In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)
To solve the problem step by step, we will prove both parts of the question regarding the areas of the parallelograms and the triangle.
1. Identify the Parallelograms: We have two parallelograms, PQRS and ABRS. Both share the same base SR.
Hint: Look for the common base and the parallel lines that define the two parallelograms.
2. Identify the Parallel Lines: The sides SR and PB are parallel lines. Since both parallelograms are between the same parallel lines (SR and PB), they occupy the same vertical space.
Hint: Recall that the area of a parallelogram is determined by its base and height.
3. Use the Area Property: The area of a parallelogram is given by the formula:
Area=Base×Height
Since both parallelograms share the same base (SR) and are between the same parallel lines, they have the same height.
Hint: Remember that if two parallelograms share the same base and height, their areas are equal.
4. Conclude the Proof: Therefore, we can conclude that:
ar(PQRS)=ar(ABRS)
(ii) Prove that ar(AXS)=12ar(PQRS)
1. Identify the Triangle and Parallelogram: We need to find the area of triangle AXS and relate it to the area of parallelogram PQRS.
Hint: Look at the base and height of triangle AXS.
2. Identify the Base and Height: Triangle AXS shares the base AS with parallelogram ABRS. The height of triangle AXS is the same as the height of parallelogram ABRS (the distance from point A to line BR).
Hint: The height of the triangle is the same as the height of the parallelogram because they are both measured from the same line.
3. Use the Area Formula for Triangle: The area of triangle AXS can be expressed as:
ar(AXS)=12×Base×Height
Here, the base is AS and the height is the same as that of parallelogram ABRS.
Hint: Remember that the area of a triangle is half the product of its base and height.
4. Relate Triangle AXS to Parallelogram ABRS: From part (i), we established that ar(ABRS)=ar(PQRS). Thus, we can write:
ar(AXS)=12ar(ABRS)
5. Substitute the Area of Parallelogram: Since ar(ABRS)=ar(PQRS), we can replace it:
ar(AXS)=12ar(PQRS)
6. Conclude the Proof: Therefore, we have shown that:
ar(AXS)=12ar(PQRS)
Final Conclusion
We have successfully proved both parts of the question:
1. ar(PQRS)=ar(ABRS)
2. ar(AXS)=12ar(PQRS)
Area=Base×Height
Since both parallelograms share the same base (SR) and are between the same parallel lines, they have the same height.
ar(PQRS)=ar(ABRS)
ar(AXS)=12×Base×Height
Here, the base is AS and the height is the same as that of parallelogram ABRS.
ar(AXS)=12ar(ABRS)
ar(AXS)=12ar(PQRS)
ar(AXS)=12ar(PQRS)
We have successfully proved both parts of the question:
1. ar(PQRS)=ar(ABRS)
2. ar(AXS)=12ar(PQRS)
Similar Questions
In Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(∣∣gmPQRS)=ar(∣∣gmABRS), ar(△AXS)=12ar(∣∣gmPQRS)
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionIn figure, PQ=PR . Show that PS>PQ.
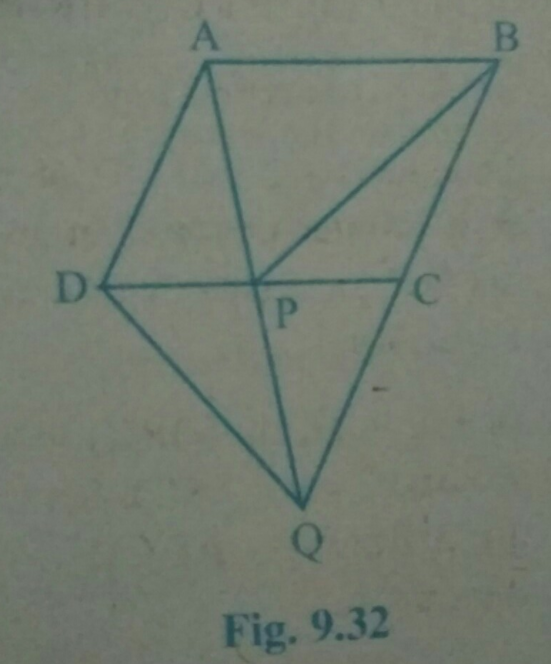
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View SolutionIn Fig. if ST∣∣QR . Find PS
View SolutionIn Figure, PQRS is a quadrilateral in which diagonals PR and QS intersect in O. Show that :
(i) PQ+QR+RS+SP>PR+QS
(ii) PQ+QR+RS+SP<2(PR+QS)
View SolutionPQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB∣∣QR . If area of △PBQ is 17 cm2, find the area of △ASR
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : (i) SR ∣∣ AC and SR=12AC (ii) PQ=SR (iii) PQRS is a parallelogram
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR. Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionIn Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
View Solution