Aarushi was driving a car with uniform speed of 60 km/h. Draw distance-time graph. From the graph, find the distance travelled by Aarushi in (i) (ii)
To solve the problem step by step, we will first derive the distance-time equation based on the given speed, then plot the graph, and finally use the graph to find the required distances.
Step 1: Establish the Relationship
Aarushi is driving at a uniform speed of 60 km/h. We can use the formula for speed:
Speed=DistanceTime
This can be rearranged to find the distance:
Distance=Speed×Time
Substituting the speed:
y=60x
where y is the distance in kilometers and x is the time in hours.
Step 2: Calculate Points for the Graph
To draw the distance-time graph, we need at least two points.
1. When x=0 (Time = 0 hours):
y=60×0=0(Distance = 0 km)
So, the first point is (0,0).
2. When x=1 (Time = 1 hour):
y=60×1=60(Distance = 60 km)
So, the second point is (1,60).
3. When x=2.5 (Time = 2.5 hours):
y=60×2.5=150(Distance = 150 km)
So, the third point is (2.5,150).
4. When x=0.5 (Time = 0.5 hours):
y=60×0.5=30(Distance = 30 km)
So, the fourth point is (0.5,30).
Step 3: Plot the Graph
Now, we can plot these points on a graph with the x-axis representing time (in hours) and the y-axis representing distance (in kilometers).
- Plot the points:
- (0,0)
- (1,60)
- (2.5,150)
- (0.5,30)
Connect these points with a straight line since the speed is uniform.
Step 4: Find Distances from the Graph
From the graph, we can now find the distances for the specified times.
(i) For 2.5 hours:
- From the graph, at x=2.5, the corresponding y value is 150 km. Therefore, the distance traveled in 2.5 hours is 150 km.
(ii) For 0.5 hours:
- From the graph, at x=0.5, the corresponding y value is 30 km. Therefore, the distance traveled in 0.5 hours is 30 km.
Summary of Results
- Distance traveled in 2.5 hours: 150 km
- Distance traveled in 0.5 hours: 30 km
Aarushi is driving at a uniform speed of 60 km/h. We can use the formula for speed:
To draw the distance-time graph, we need at least two points.
y=60×0=0(Distance = 0 km)
So, the first point is (0,0).
y=60×1=60(Distance = 60 km)
So, the second point is (1,60).
y=60×2.5=150(Distance = 150 km)
So, the third point is (2.5,150).
y=60×0.5=30(Distance = 30 km)
So, the fourth point is (0.5,30).
Now, we can plot these points on a graph with the x-axis representing time (in hours) and the y-axis representing distance (in kilometers).
- (0,0)
- (1,60)
- (2.5,150)
- (0.5,30)
From the graph, we can now find the distances for the specified times.
- From the graph, at x=2.5, the corresponding y value is 150 km. Therefore, the distance traveled in 2.5 hours is 150 km.
- From the graph, at x=0.5, the corresponding y value is 30 km. Therefore, the distance traveled in 0.5 hours is 30 km.
- Distance traveled in 2.5 hours: 150 km
- Distance traveled in 0.5 hours: 30 km
Topper's Solved these Questions
Similar Questions
A car travels for 20 min with a constant speed of 54 km h−1 Find the distance travelled by the car.
View SolutionIf the speed of a car is 10515 km/h, find the distance covered by it in 335 hours.
View SolutionFind the distance covered by a car in 2(25) hours at a speed of 46(23) km per hour.
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
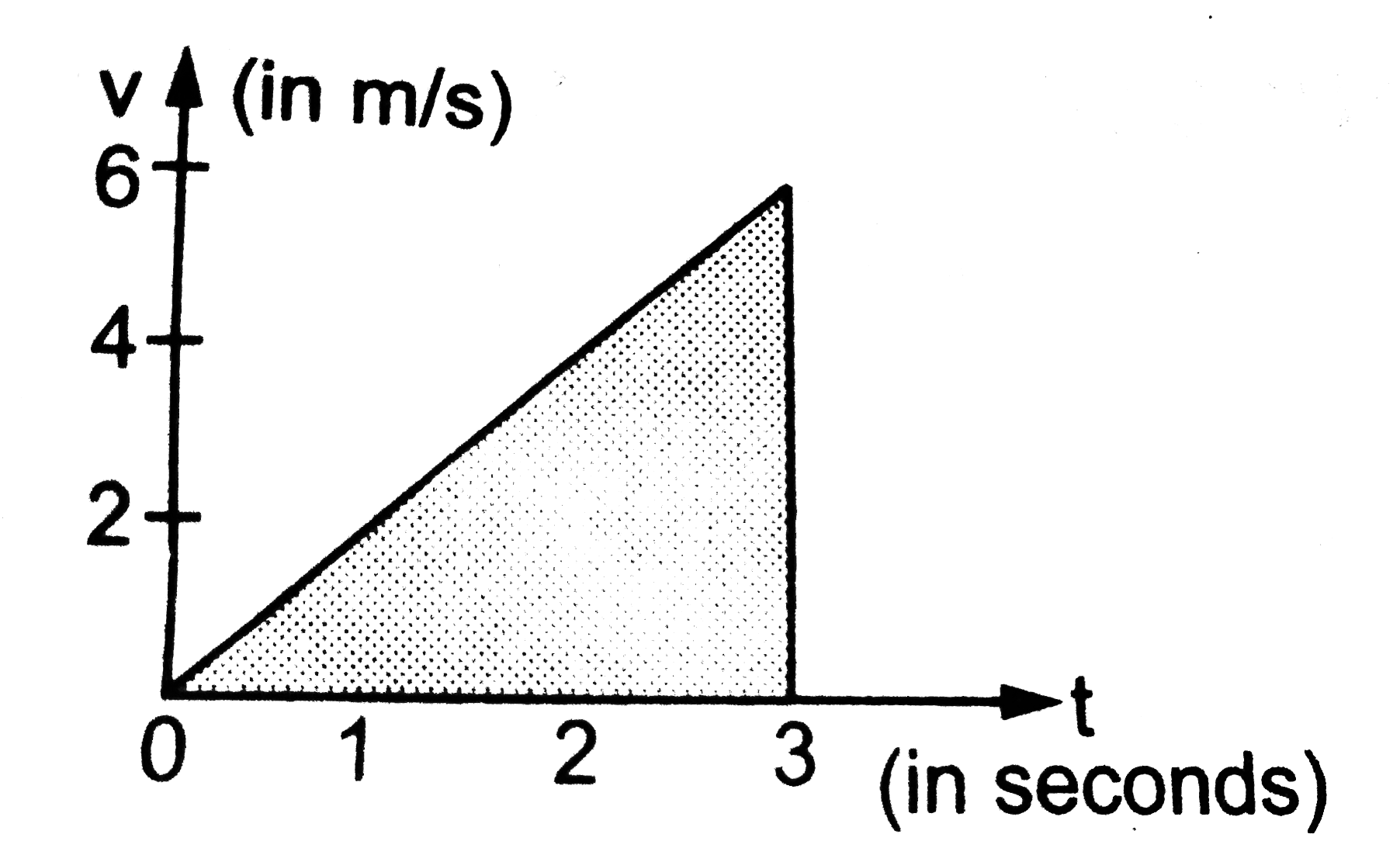
View SolutionA driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he ils driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0ms2, find the distance travelled by the car after he sees the need to put the brakes on.
View SolutionA bus starting from rest moves with a uniform acceleration of 0.1m/s2 for 2 minutes. Find
(a) the speed acquired, (b) the distance travelled.
View SolutionA car starting from rest accelerates uniformly to acquire a speed 20 km h−1 in 30 min. The distance travelled by car in this time interval will be :
View SolutionA train travels a distance of 300 km with an average speed of 60 kmh−1 . How much time does it take to cover the distance ?
View SolutionA man rides a cycle at a speed of 6313km/h. Find the distance travelled in 213 hours.
View SolutionA car travels with a uniform velocity of 20 m s−1 for 5 s. The brakes are then applied and the car is uniformly retarded. It comes to rest in further 8 s. Draw a graph of velocity against time. Use this graph to find :
(i) the distance travelled in first 5 s,
(ii) the distance travelled after the brakes are applied,
(iii) total distance travelled, and
(iv) acceleration during the first 5 s and last 8 s.
View Solution
