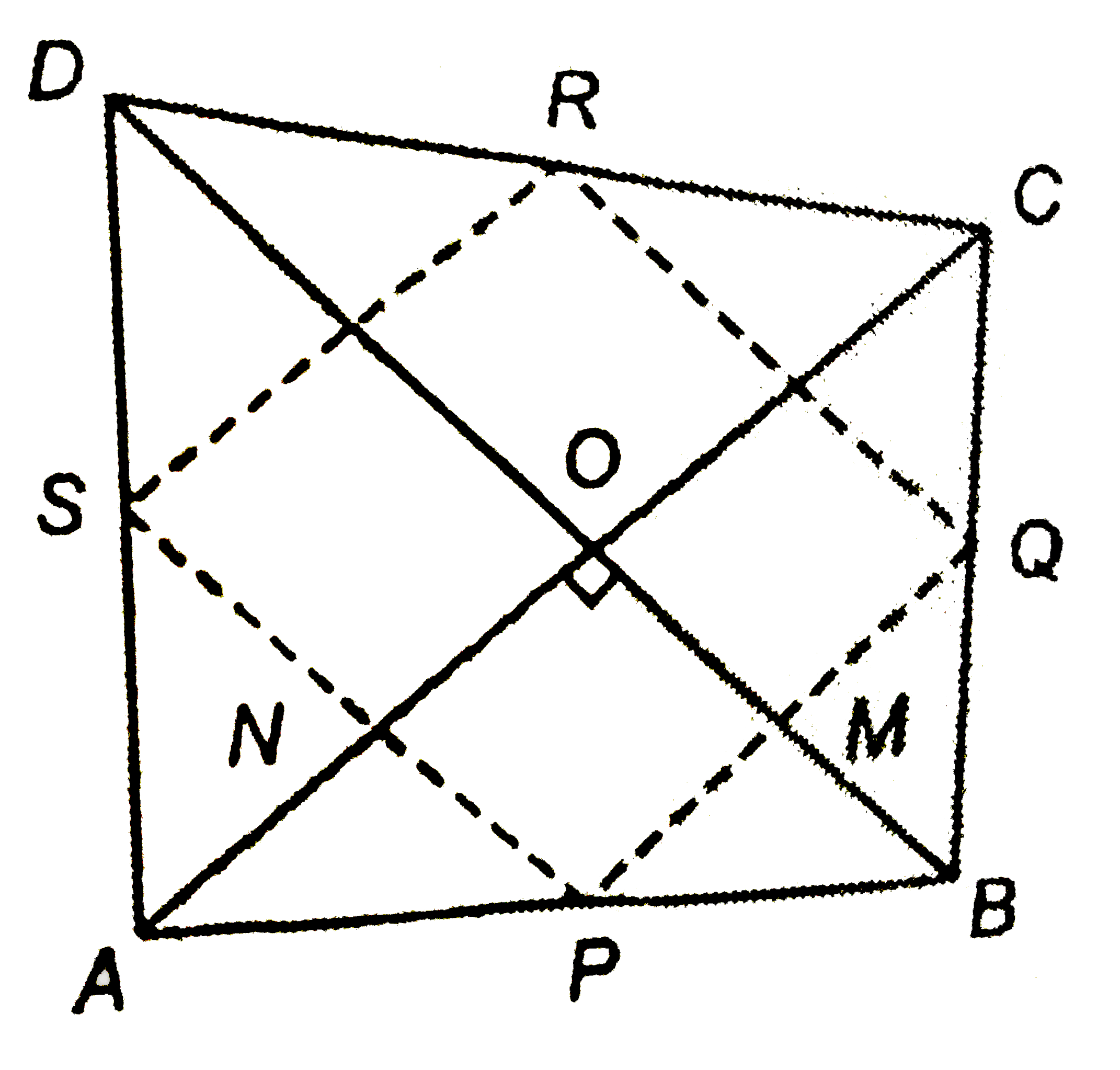
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
To prove that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD (where the diagonals AC and BD are perpendicular) is a rectangle, we will follow these steps:
Step 1: Identify the Midpoints
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA respectively.
Step 2: Prove PQ is Parallel to SR
In triangle ABC, since P is the midpoint of AB and Q is the midpoint of BC, by the Midpoint Theorem, we have:
PQ∥AC
and
PQ=12AC
In triangle ACD, since S is the midpoint of AD and R is the midpoint of CD, we also have:
SR∥AC
and
SR=12AC
Since both PQ and SR are parallel to AC and equal in length, we conclude:
PQ∥SRandPQ=SR
Step 3: Prove PS is Parallel to QR
Now, consider triangle ABD. Since P is the midpoint of AB and S is the midpoint of AD, by the Midpoint Theorem:
PS∥BD
and
PS=12BD
In triangle BCD, since Q is the midpoint of BC and R is the midpoint of CD, we have:
QR∥BD
and
QR=12BD
Since both PS and QR are parallel to BD and equal in length, we conclude:
PS∥QRandPS=QR
Step 4: Conclude that PQRS is a Parallelogram
Since we have shown that:
1. PQ∥SR and PQ=SR
2. PS∥QR and PS=QR
This means that quadrilateral PQRS is a parallelogram.
Step 5: Show that One Angle is 90 Degrees
Now, we need to show that one angle of the parallelogram PQRS is 90 degrees. Since diagonals AC and BD of quadrilateral ABCD are perpendicular, we have:
∠APB=90∘
This means that:
∠SPQ=∠APB=90∘
Step 6: Conclude that PQRS is a Rectangle
Since PQRS is a parallelogram and one of its angles (angle SPQ) is 90 degrees, it follows that all angles in the parallelogram are 90 degrees. Therefore, PQRS is a rectangle.
Thus, we have shown that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD is a rectangle.
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA respectively.
In triangle ABC, since P is the midpoint of AB and Q is the midpoint of BC, by the Midpoint Theorem, we have:
PQ∥AC
and
PQ=12AC
SR∥AC
and
SR=12AC
PQ∥SRandPQ=SR
Now, consider triangle ABD. Since P is the midpoint of AB and S is the midpoint of AD, by the Midpoint Theorem:
PS∥BD
and
PS=12BD
QR∥BD
and
QR=12BD
PS∥QRandPS=QR
Since we have shown that:
1. PQ∥SR and PQ=SR
2. PS∥QR and PS=QR
Now, we need to show that one angle of the parallelogram PQRS is 90 degrees. Since diagonals AC and BD of quadrilateral ABCD are perpendicular, we have:
∠APB=90∘
This means that:
∠SPQ=∠APB=90∘
Since PQRS is a parallelogram and one of its angles (angle SPQ) is 90 degrees, it follows that all angles in the parallelogram are 90 degrees. Therefore, PQRS is a rectangle.
Topper's Solved these Questions
Similar Questions
Show that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View Solution(−2,4),(4,8),(10,7) and (11,−5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
View SolutionProve that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
View Solution