The consecutive sides of a quadrilateral have (a) no common point (b) one common point (c) two common points (d) Infinitely many common points
To solve the question regarding the consecutive sides of a quadrilateral, let’s analyze the concept of consecutive sides and their intersections step by step.
1. Understanding Consecutive Sides:
- Consecutive sides of a quadrilateral are sides that share a common vertex. For example, in quadrilateral ABCD, the consecutive sides can be AB and BC, BC and CD, CD and DA, or DA and AB.
2. Identifying Points of Intersection:
- We need to determine how many common points exist between pairs of consecutive sides.
- For instance, if we take sides AB and BC, they meet at point B, which is one common point.
3. Analyzing All Pairs of Consecutive Sides:
- Let's analyze the pairs:
- AB and BC: Common point at B.
- BC and CD: Common point at C.
- CD and DA: Common point at D.
- DA and AB: Common point at A.
- Each pair of consecutive sides intersects at exactly one point, which is the vertex they share.
4. Conclusion:
- Since each pair of consecutive sides has exactly one common point, we conclude that the consecutive sides of a quadrilateral have one common point.
5. Final Answer:
- Therefore, the correct option is (b) one common point.
- Consecutive sides of a quadrilateral are sides that share a common vertex. For example, in quadrilateral ABCD, the consecutive sides can be AB and BC, BC and CD, CD and DA, or DA and AB.
- We need to determine how many common points exist between pairs of consecutive sides.
- For instance, if we take sides AB and BC, they meet at point B, which is one common point.
- Let's analyze the pairs:
- AB and BC: Common point at B.
- BC and CD: Common point at C.
- CD and DA: Common point at D.
- DA and AB: Common point at A.
- Each pair of consecutive sides intersects at exactly one point, which is the vertex they share.
- Since each pair of consecutive sides has exactly one common point, we conclude that the consecutive sides of a quadrilateral have one common point.
- Therefore, the correct option is (b) one common point.
Topper's Solved these Questions
Similar Questions
The opposite sides of a quadrilateral have (a) no common point (b) one common point (c) two common points (d) Infinitely many common points
View Solution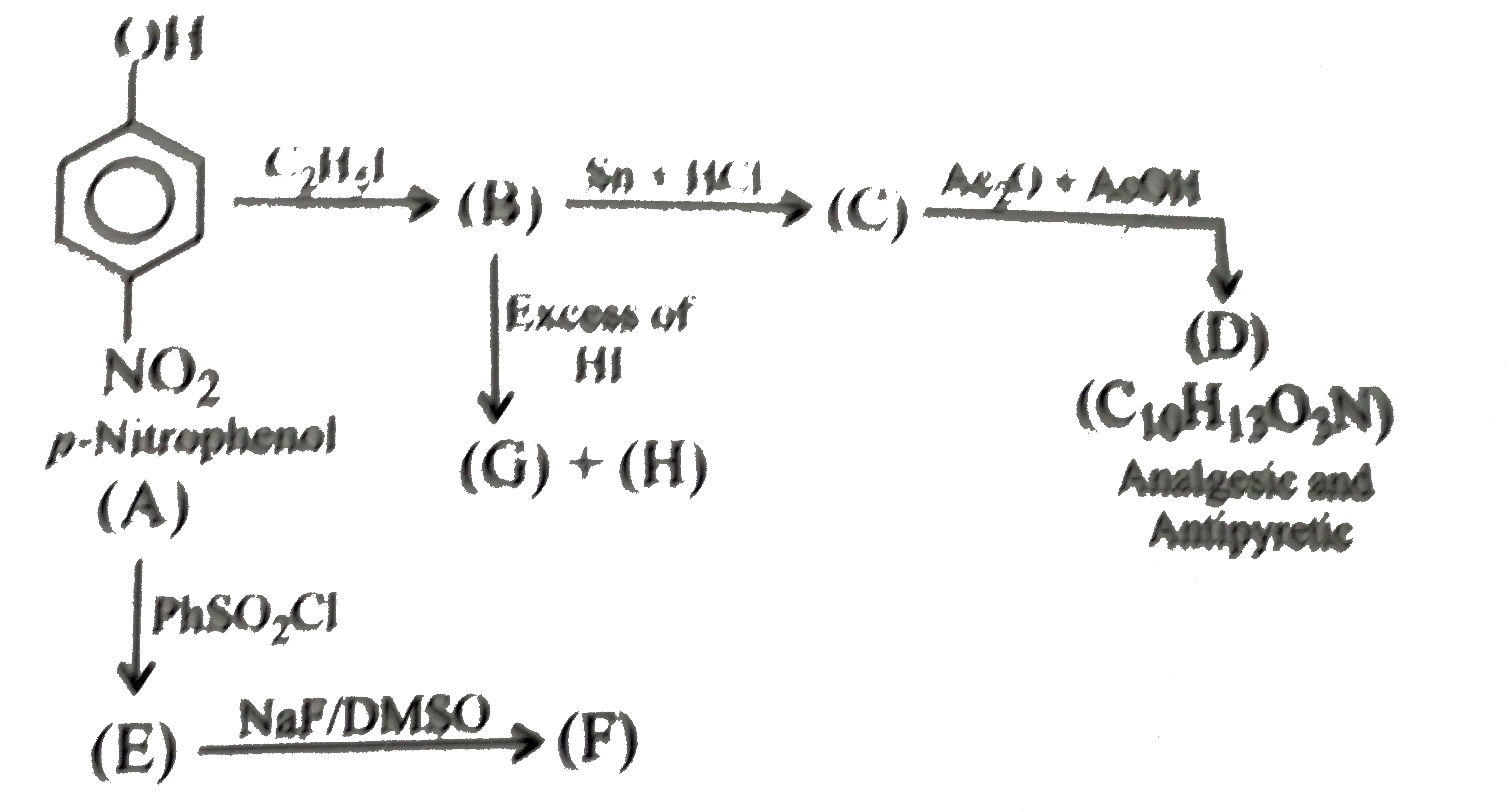
The common name of the compound (D) is:
View SolutionDraw rough diagrams of two angles such that they have a) One point in common.(b) Two points in common.(c) Three points in common.(d) Four points in common.(e) One ray in common
View SolutionThe inflorescence where flowers arise from a common point, is known as
View SolutionAll algae have two photosynthetic pigments in common
View SolutionTwo distinct .......... in a plane cannot have more than one point in common.
View SolutionThe mid-point of the line joining the common points of the line 2x−3y+8=0 and y2=8x, is
View SolutionEichhornia and Vallisneria are common in having
View SolutionEichhornia and Vallisneria are common in having
View SolutionDraw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
View Solution
