Show that the bisectors of angles of a parallelogram form a rectangle.
Step by step video & image solution for Show that the bisectors of angles of a parallelogram form a rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The angle bisectors of a parallelogram form a rectangle.
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View Solution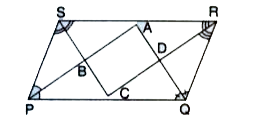
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionProve that the bisectors of opposite angles of a parallelogram are parallel.
View SolutionAB and CD are two parallel lines and a transversal 'l' intersects these lines at X and Y respectively Prove that the bisectors of interior angles from a parallelogram whose each angle is 90∘.
View SolutionThe opposite angles of a parallelogram are equal.
View SolutionIf the two diagonals of a parallelogram are equal, it is a rectangle.
View SolutionShow that, in a parallelogram ABCD, the internal and external bisectors of ∠Aand∠B from a rectangle.
View SolutionProve that the bisectors of the interior angles of a rectangle form a square.
View Solution
