In Figure, compute the area of quadrilateral ABCD.
To compute the area of quadrilateral ABCD, we can break it down into two triangles: triangle ABD and triangle BCD. We will use the formula for the area of a triangle, which is:
Area=12×base×height
Step 1: Calculate the area of triangle ABD
1. Identify the base and height:
- Let AB be the base and AD be the height.
- Given: AD=9cm
2. Find the length of AB:
- We will find AB using the Pythagorean theorem in triangle ABD.
- We need to find BD first.
Step 2: Calculate the length of BD using triangle BCD
1. Identify the sides:
- Given: BC=8cm and CD=17cm (hypotenuse).
2. Apply the Pythagorean theorem:
CD2=BC2+BD2
172=82+BD2
289=64+BD2
BD2=289−64=225
BD=√225=15cm
Step 3: Calculate the length of AB using triangle ABD
1. Apply the Pythagorean theorem again:
- Now we know BD=15cm and AD=9cm.
BD2=AB2+AD2
152=AB2+92
225=AB2+81
AB2=225−81=144
AB=√144=12cm
Step 4: Calculate the area of triangle ABD
1. Use the area formula:
AreaABD=12×AB×AD=12×12×9
=6×9=54cm2
Step 5: Calculate the area of triangle BCD
1. Use the area formula:
AreaBCD=12×BC×BD=12×8×15
=4×15=60cm2
Step 6: Calculate the total area of quadrilateral ABCD
1. Add the areas of triangles ABD and BCD:
AreaABCD=AreaABD+AreaBCD=54+60
=114cm2
Conclusion
Hence, the area of quadrilateral ABCD is 114cm2.
---
- Let AB be the base and AD be the height.
- Given: AD=9cm
- We will find AB using the Pythagorean theorem in triangle ABD.
- We need to find BD first.
- Given: BC=8cm and CD=17cm (hypotenuse).
CD2=BC2+BD2
172=82+BD2
289=64+BD2
BD2=289−64=225
BD=√225=15cm
- Now we know BD=15cm and AD=9cm.
BD2=AB2+AD2
152=AB2+92
225=AB2+81
AB2=225−81=144
AB=√144=12cm
AreaABD=12×AB×AD=12×12×9
=6×9=54cm2
AreaBCD=12×BC×BD=12×8×15
=4×15=60cm2
AreaABCD=AreaABD+AreaBCD=54+60
=114cm2
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a quadrilateral and BE∣∣AC and also BE meets DC produced at E . Show that area of △ADE is equal to the area of the quadrilateral ABCD.
View SolutionIn Figure, ABCD is a quadrilateral and BE∣AC and also BE meets DC produced at E. Show that area of ADE is equal to the area of the quadrilateral ABCD
View Solution
Knowledge Check
- Question 1 - Select One
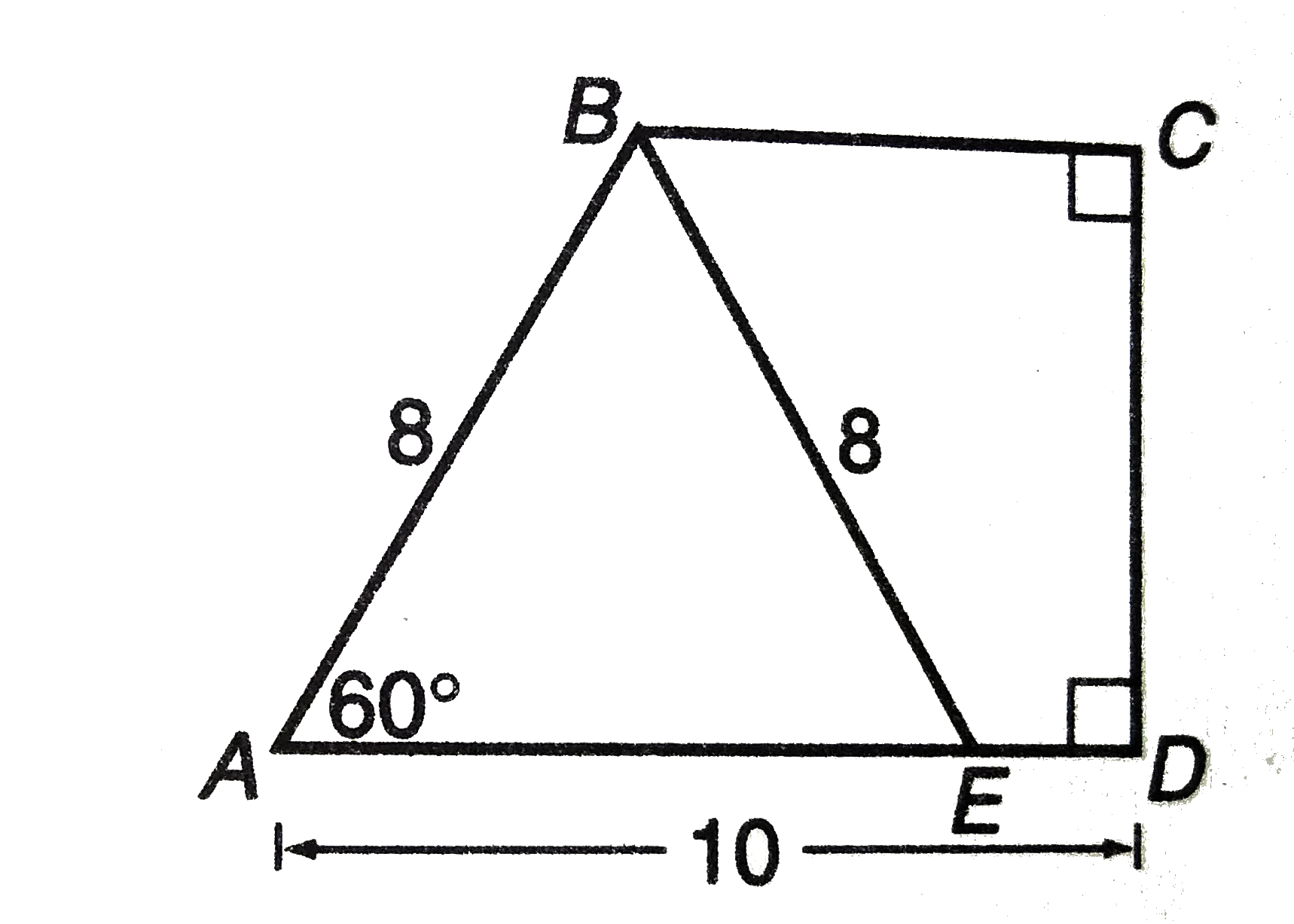
In the figure above, what is the area of quadrilateral BCDE?A8√3B16√3C8+4√3D4+12√3 - Question 2 - Select One
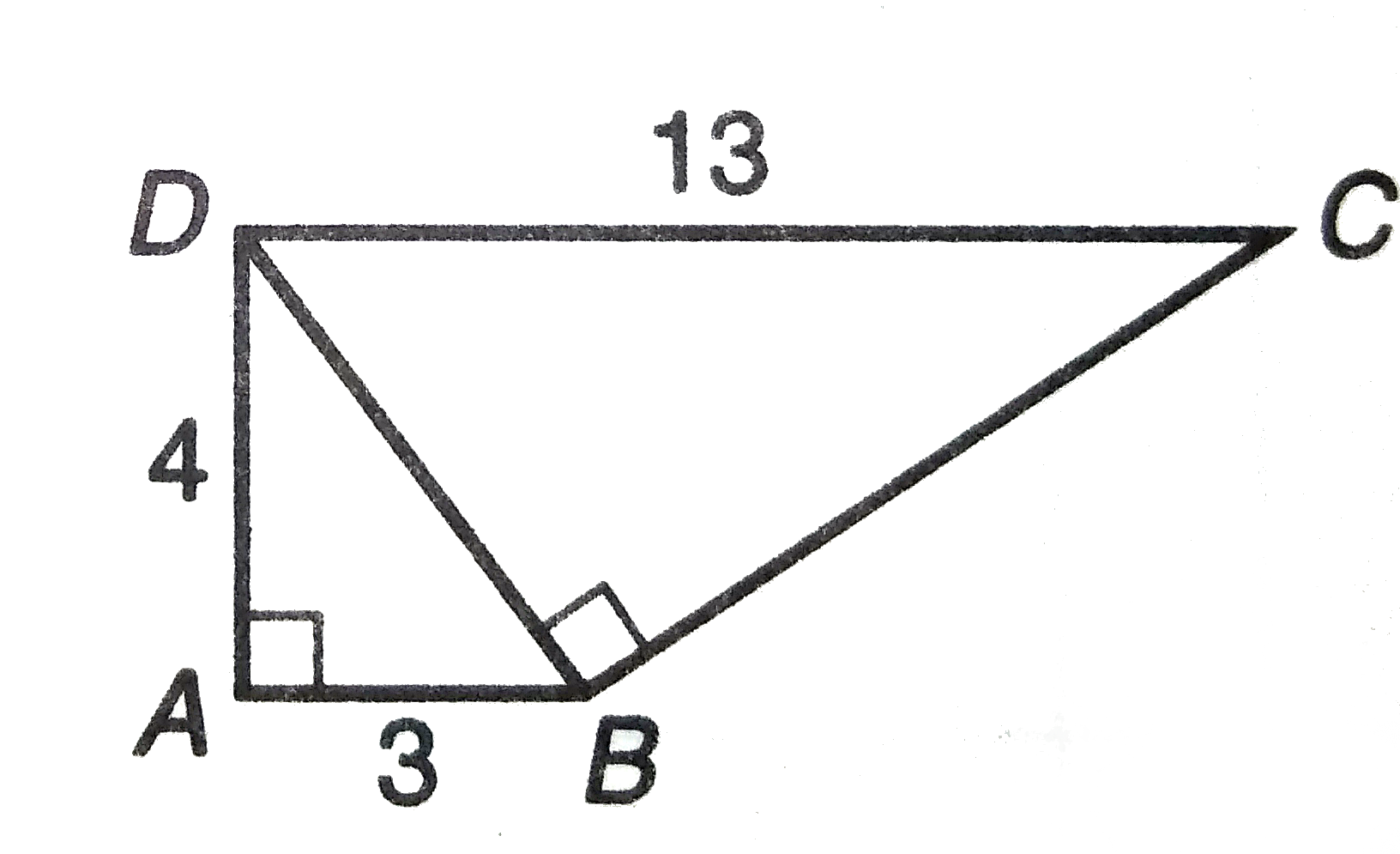
In the figure above, what is the area of quadrilateral ABCD?A28B32C36D42 - Question 3 - Select One
In the figure, the area of the quadrilateral ABCD is 75. What is the area of parallelogram EFGH?
 A96B153C157D171
A96B153C157D171
In Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionIn the adjoining figure ABDC and DA is perpendicular to AB. Further, DC=7cm, CB=10cm and AB=13cm. Find the area of the quadrilateral ABCD.
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD.
View SolutionIf A(−5, 7), B(−4, −5), C(−1, −6) and D(4, 5)are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View Solution

