In Figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10cm. If OE=2√5cm , find the area of the rectangle.
To solve the problem, we need to find the area of the rectangle OCDE inscribed in a quadrant of a circle with a radius of 10cm and given that OE=2√5cm.
1. Identify the Given Information:
- Radius of the circle, OD=10cm
- Length of one side of the rectangle, OE=2√5cm
2. Define the Dimensions of the Rectangle:
- Let the breadth of the rectangle OCDE be OE.
- Let the length of the rectangle ED be denoted as x.
3. Apply the Pythagorean Theorem:
- In triangle OED, we can apply the Pythagorean theorem. The relationship is given by:
OD2=OE2+ED2
- Substituting the known values:
102=(2√5)2+x2
- This simplifies to:
100=20+x2
4. Solve for x2:
- Rearranging the equation gives:
x2=100−20=80
5. Calculate x:
- Taking the square root of both sides:
x=√80=4√5cm
6. Calculate the Area of the Rectangle:
- The area A of rectangle OCDE is given by:
A=length×breadth=ED×OE
- Substituting the values we found:
A=(4√5)×(2√5)=8×5=40cm2
7. Conclusion:
- Therefore, the area of rectangle OCDE is:
40cm2
- Radius of the circle, OD=10cm
- Length of one side of the rectangle, OE=2√5cm
- Let the breadth of the rectangle OCDE be OE.
- Let the length of the rectangle ED be denoted as x.
- In triangle OED, we can apply the Pythagorean theorem. The relationship is given by:
OD2=OE2+ED2
- Substituting the known values:
102=(2√5)2+x2
- This simplifies to:
100=20+x2
- Rearranging the equation gives:
x2=100−20=80
- Taking the square root of both sides:
x=√80=4√5cm
- The area A of rectangle OCDE is given by:
A=length×breadth=ED×OE
- Substituting the values we found:
A=(4√5)×(2√5)=8×5=40cm2
- Therefore, the area of rectangle OCDE is:
40cm2
Topper's Solved these Questions
Similar Questions
In Figure , a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region
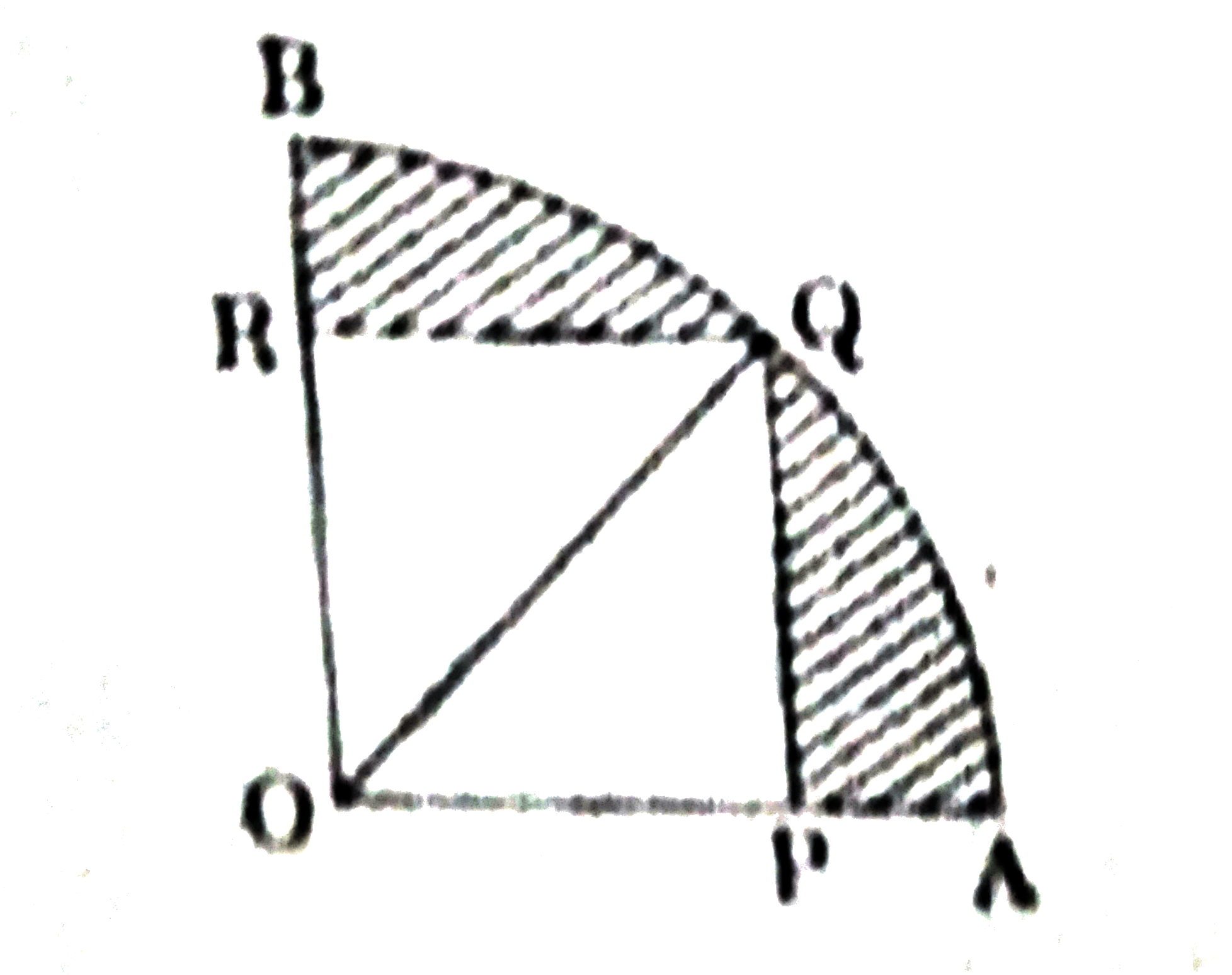
View SolutionIn Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View SolutionA rectangle in inscribed in a circle of radius 5 cm. if the breadth of the rectangle is 6 cm. then find the length of the rectangle.
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13cm. A is any point on PQ. If PS=5cm, then find ar ( RAS)
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2 cm , find the area of the (i) quadrant OACB (ii) shaded region.
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIf an isosceles triangle ABC in which AB=AC=6cm is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionIf an isosceles ΔABC in which AB=AC=6cm, is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionArea of a rectangle of breadth 17cm is 340cm2. Find the perimeter of the rectangle.
View Solution
