Given an arc of a circle, complete the circle.
To complete a circle given an arc, follow these steps:
1. Identify the Arc: Let the given arc be denoted as PQ.
2. Choose a Point on the Arc: Select a point R on the arc PQ.
3. Join Points: Draw line segments PR and QR by connecting points P and R, and Q and R.
4. Construct Perpendicular Bisectors:
- To find the perpendicular bisector of PR:
- Use a compass to measure the distance from point P to point R.
- With the same measurement, draw arcs above and below the line segment PR from both points P and R.
- Label the intersection points of the arcs as A and B.
- Draw a line through points A and B. This line is the perpendicular bisector of PR.
- To find the perpendicular bisector of QR:
- Repeat the same process with points Q and R.
- Measure the distance from Q to R and draw arcs above and below the line segment QR from both points Q and R.
- Label the intersection points of these arcs as C and D.
- Draw a line through points C and D. This line is the perpendicular bisector of QR.
5. Find the Center of the Circle: The point where the two perpendicular bisectors intersect is the center of the circle. Let this point be O.
6. Determine the Radius: Measure the distance from point O to either point P or Q (which will be the same) to find the radius of the circle.
7. Draw the Circle: Using a compass, set the radius to the distance OP (or OQ) and draw the circle centered at point O.
Final Result:
You have now completed the circle that contains the arc PQ.
---
- To find the perpendicular bisector of PR:
- Use a compass to measure the distance from point P to point R.
- With the same measurement, draw arcs above and below the line segment PR from both points P and R.
- Label the intersection points of the arcs as A and B.
- Draw a line through points A and B. This line is the perpendicular bisector of PR.
- To find the perpendicular bisector of QR:
- Repeat the same process with points Q and R.
- Measure the distance from Q to R and draw arcs above and below the line segment QR from both points Q and R.
- Label the intersection points of these arcs as C and D.
- Draw a line through points C and D. This line is the perpendicular bisector of QR.
You have now completed the circle that contains the arc PQ.
Topper's Solved these Questions
Similar Questions
. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
View SolutionIf the locus of the complex number z given by arg(z+i)−arg(z−i)=2π3 is an arc of a circle, then the length of the arc is
View SolutionThe locus of the centre of a circle the touches the given circle externally is a _______
View SolutionAn arc of length 20π cm subtends an angle of 144o at the centre of a circle. Find the radius of the circle.
View SolutionThe radius of a circle is 50 cm. Find the angle subtends by an arc of 22 cm length at the centerof the circle.
View SolutionAn arc 15 ft long describes an angle of 5 radians at the centre of a circle. Find the radius of the circle.
View Solution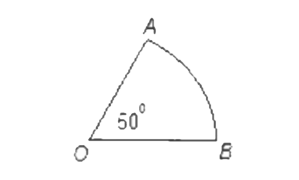
In the figure abvoe, aB is the arc of a circle with centre O. If the length of arc AB is 4π, what is the area of region OAB to the nearest tenth?
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View Solution
