L and M are mid-point of two equal chords AB and CD of a circle with centre O . Prove that ∠OLM= ∠OML (ii) ∠ALM= ∠CML
To prove the statements given in the question, we will follow a systematic approach.
1. Draw the Circle and Chords:
- Draw a circle with center O.
- Draw two equal chords AB and CD such that AB=CD.
Hint: Remember that equal chords in a circle are equidistant from the center.
2. Identify Midpoints:
- Let L be the midpoint of chord AB.
- Let M be the midpoint of chord CD.
Hint: The midpoints divide the chords into two equal segments.
3. Draw Perpendiculars from Center:
- Draw perpendicular lines from the center O to the chords AB and CD. Let these perpendiculars meet AB at point P and CD at point Q.
Hint: A line drawn from the center of a circle to a chord is always perpendicular to that chord.
4. Establish Equal Distances:
- Since AB and CD are equal chords, the distances from the center O to the chords (i.e., OP and OQ) must also be equal. Thus, OP=OQ.
Hint: Use the property of equal chords to establish that the distances from the center are equal.
5. Show OL=OM:
- Since L and M are midpoints, we have AL=LB and CM=MD. Therefore, triangles OLA and OMC are right triangles with equal hypotenuses OA=OC and equal legs OP=OQ.
Hint: Use the properties of triangles to show that the lengths of the segments from the center to the midpoints are equal.
6. Prove Angles OLM and OML are Equal:
- In triangle OLM, since OL=OM (from the previous step), by the Isosceles Triangle Theorem, we have ∠OLM=∠OML.
Hint: Recall that angles opposite equal sides in a triangle are equal.
7. Prove Angles ALM and CML are Equal:
- Since ∠OLA=90∘ and ∠OMC=90∘ (perpendiculars from the center), we can express:
∠ALM=∠OLA−∠OLM
∠CML=∠OMC−∠OML
- Since ∠OLA=∠OMC and ∠OLM=∠OML, we can conclude that:
∠ALM=∠CML
Hint: Use the properties of angles in right triangles to establish the equality of the angles.
Conclusion:
We have shown that ∠OLM=∠OML and ∠ALM=∠CML as required.
- Draw a circle with center O.
- Draw two equal chords AB and CD such that AB=CD.
- Let L be the midpoint of chord AB.
- Let M be the midpoint of chord CD.
- Draw perpendicular lines from the center O to the chords AB and CD. Let these perpendiculars meet AB at point P and CD at point Q.
- Since AB and CD are equal chords, the distances from the center O to the chords (i.e., OP and OQ) must also be equal. Thus, OP=OQ.
- Since L and M are midpoints, we have AL=LB and CM=MD. Therefore, triangles OLA and OMC are right triangles with equal hypotenuses OA=OC and equal legs OP=OQ.
- In triangle OLM, since OL=OM (from the previous step), by the Isosceles Triangle Theorem, we have ∠OLM=∠OML.
- Since ∠OLA=90∘ and ∠OMC=90∘ (perpendiculars from the center), we can express:
∠ALM=∠OLA−∠OLM
∠CML=∠OMC−∠OML
- Since ∠OLA=∠OMC and ∠OLM=∠OML, we can conclude that:
∠ALM=∠CML
We have shown that ∠OLM=∠OML and ∠ALM=∠CML as required.
Topper's Solved these Questions
Similar Questions
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
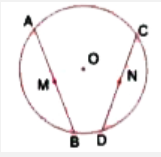
∠AMN=∠CNM.
View SolutionIn a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
View SolutionIn a △ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( △LCM)=ar (△LBM)
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( LOB)=ar ( MOC).
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( ABM)=ar ( ACL).
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that:
(i) PL=QM
(ii) LO=OM
View SolutionTwo chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD
View SolutionIn A PQR, if PQ=QR and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
View SolutionIn Figure, equal chords AB and CD of a circle with centre O, cut at right angles at E. If M and N are mid-point of AB and CD respectively, prove that OMEN is a square.
View Solution
