Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
AB=CD.
AB is not equal to CD.
AB there is no relation between CD.
AB is greater than CD.
The correct Answer is:A
To solve the problem, we need to show that the lengths of the two chords AB and CD are equal, given that both are at a distance of 4 cm from the center of the circle.
1. Draw the Circle and Chords:
- Draw a circle with center O.
- Draw two chords AB and CD such that both are at a distance of 4 cm from the center O.
2. Identify the Perpendiculars:
- Draw a perpendicular line from the center O to chord AB, and let the foot of the perpendicular be point L.
- Similarly, draw a perpendicular line from O to chord CD, and let the foot of the perpendicular be point M.
3. Label the Distances:
- According to the problem, the distance OL (from O to chord AB) is 4 cm.
- The distance OM (from O to chord CD) is also 4 cm.
4. Use the Properties of Triangles:
- In triangle OLB, OB is the radius of the circle, and in triangle OMD, OD is also the radius of the circle. Therefore, OB = OD.
- Since OL = OM = 4 cm, we have OL = OM.
5. Angles in the Triangles:
- The angles ∠OLB and ∠OMD are both right angles (90 degrees) because we drew perpendiculars from the center to the chords.
6. Congruent Triangles:
- By the Side-Angle-Side (SAS) congruence criterion, triangles OLB and OMD are congruent since:
- OB = OD (radii of the circle),
- OL = OM (both are 4 cm),
- ∠OLB = ∠OMD = 90°.
- Therefore, we can conclude that triangle OLB ≅ triangle OMD.
7. Corresponding Parts of Congruent Triangles:
- Since the triangles are congruent, the corresponding sides are equal. Thus, LB = MD.
8. Relate Chord Lengths to Segments:
- From the property of circles, we know that the perpendicular from the center of a circle bisects the chord. Therefore:
- The length of chord AB can be expressed as AB = 2 * LB.
- The length of chord CD can be expressed as CD = 2 * MD.
9. Equate the Lengths:
- Since LB = MD, we can substitute:
- AB = 2 * LB and CD = 2 * MD ⇒ AB = CD.
10. Conclusion:
- Hence, we have proved that the lengths of the chords AB and CD are equal.
Final Answer:
AB = CD
- Draw a circle with center O.
- Draw two chords AB and CD such that both are at a distance of 4 cm from the center O.
- Draw a perpendicular line from the center O to chord AB, and let the foot of the perpendicular be point L.
- Similarly, draw a perpendicular line from O to chord CD, and let the foot of the perpendicular be point M.
- According to the problem, the distance OL (from O to chord AB) is 4 cm.
- The distance OM (from O to chord CD) is also 4 cm.
- In triangle OLB, OB is the radius of the circle, and in triangle OMD, OD is also the radius of the circle. Therefore, OB = OD.
- Since OL = OM = 4 cm, we have OL = OM.
- The angles ∠OLB and ∠OMD are both right angles (90 degrees) because we drew perpendiculars from the center to the chords.
- By the Side-Angle-Side (SAS) congruence criterion, triangles OLB and OMD are congruent since:
- OB = OD (radii of the circle),
- OL = OM (both are 4 cm),
- ∠OLB = ∠OMD = 90°.
- Therefore, we can conclude that triangle OLB ≅ triangle OMD.
- Since the triangles are congruent, the corresponding sides are equal. Thus, LB = MD.
- From the property of circles, we know that the perpendicular from the center of a circle bisects the chord. Therefore:
- The length of chord AB can be expressed as AB = 2 * LB.
- The length of chord CD can be expressed as CD = 2 * MD.
- Since LB = MD, we can substitute:
- AB = 2 * LB and CD = 2 * MD ⇒ AB = CD.
- Hence, we have proved that the lengths of the chords AB and CD are equal.
AB = CD
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.3
Explore 20 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.4
Explore 14 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.4
Explore 14 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.4 Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
Similar Questions
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is 15 cm (b) 16 cm (c) 17 cm (d) 34 cm
View SolutionA chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
View SolutionA chord of length 24 cm is at a distance of 5 cm form the centre of the circle. Find the length of another chord of circle which is at a distance of 12 cm from the centre.
View SolutionIn the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
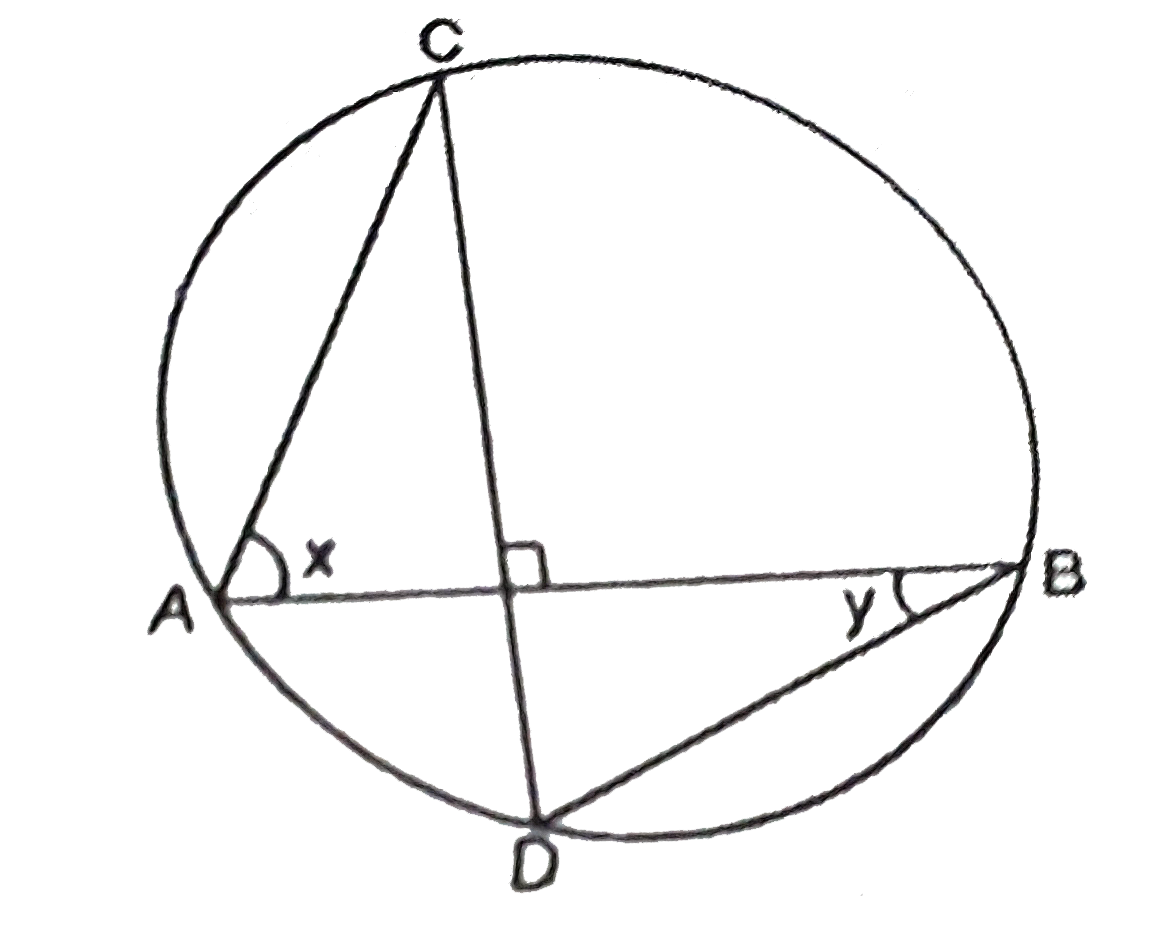
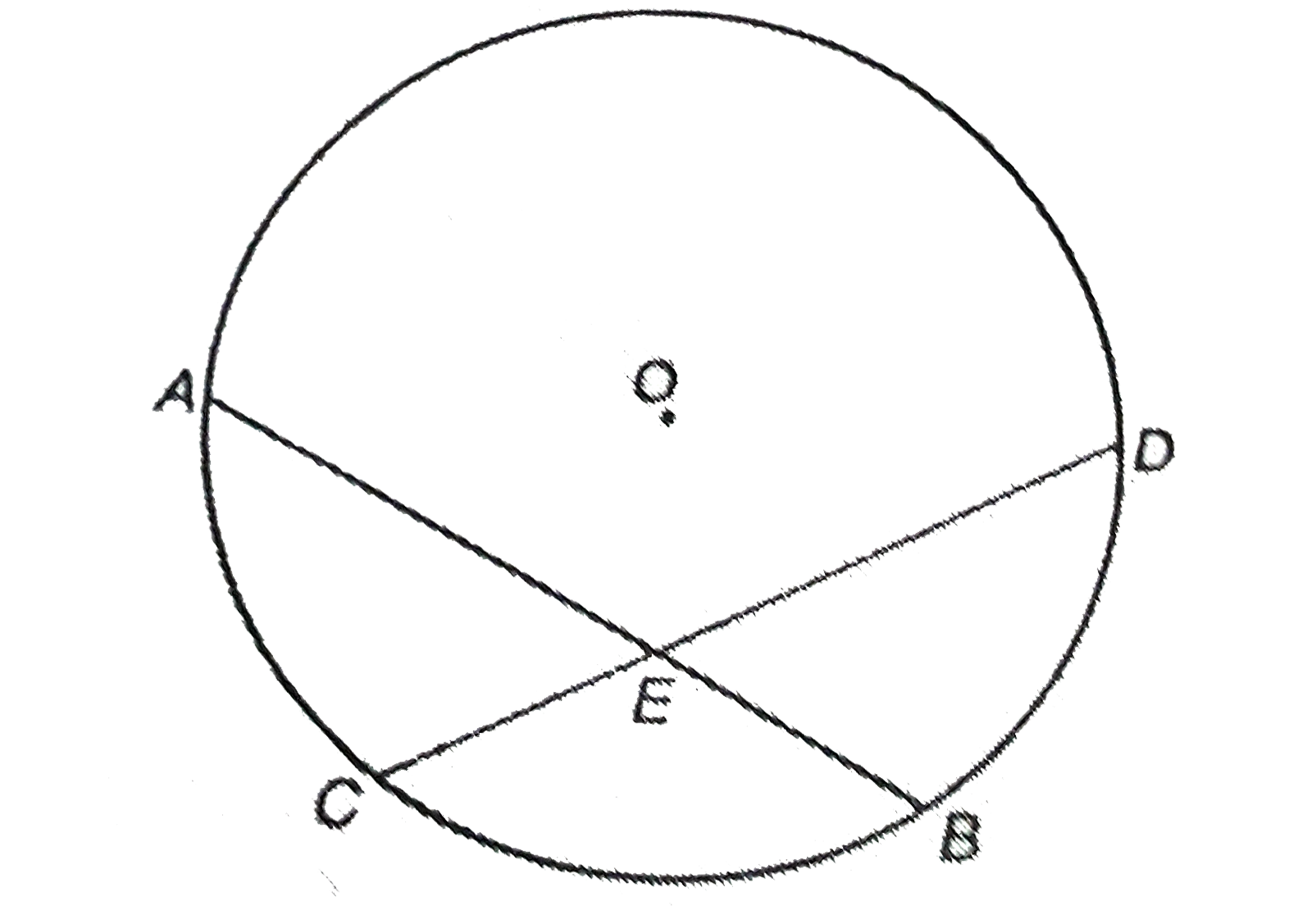
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.
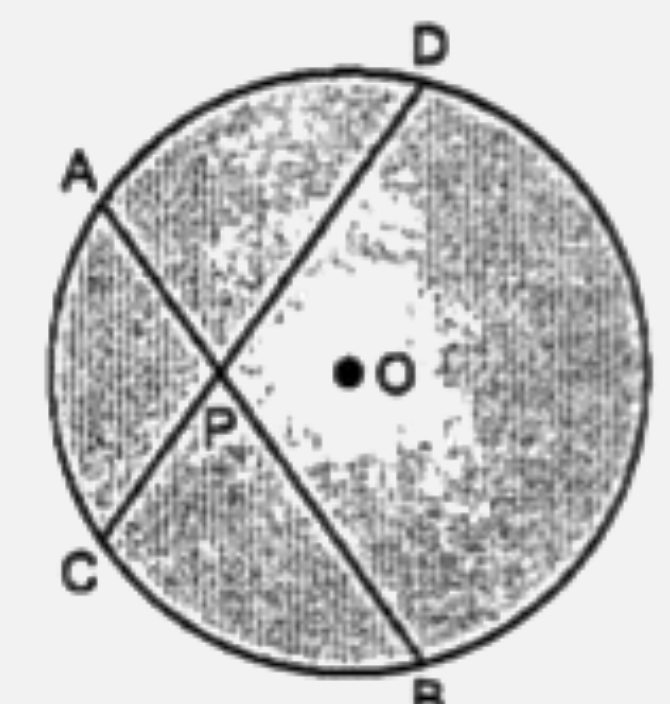
Prove that:
BP=DP
View SolutionFind the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
View Solution