The linear inequality |x|≤5 of which write the solution set and draw graph.
To solve the linear inequality |x|≤5, we will break it down step by step.
Step 1: Understand the Absolute Value Inequality
The inequality |x|≤5 means that the distance of x from 0 on the number line is at most 5. This can be interpreted as:
−5≤x≤5
Step 2: Write the Solution Set
From the interpretation above, we can write the solution set as:
{x∈R:−5≤x≤5}
This means that x can take any value between -5 and 5, inclusive.
Step 3: Graph the Solution Set
To graph the solution set on a number line:
1. Draw a horizontal line to represent the number line.
2. Mark the points -5 and 5 on the line.
3. Since the inequality includes equal to (≤), we will use solid dots at -5 and 5 to indicate that these points are included in the solution set.
4. Shade the region between -5 and 5 to represent all the values of x that satisfy the inequality.
Final Solution
The solution set is:
{x:−5≤x≤5}
And the graph will show a solid line segment between -5 and 5, inclusive.
---
The inequality |x|≤5 means that the distance of x from 0 on the number line is at most 5. This can be interpreted as:
−5≤x≤5
From the interpretation above, we can write the solution set as:
{x∈R:−5≤x≤5}
This means that x can take any value between -5 and 5, inclusive.
To graph the solution set on a number line:
1. Draw a horizontal line to represent the number line.
2. Mark the points -5 and 5 on the line.
3. Since the inequality includes equal to (≤), we will use solid dots at -5 and 5 to indicate that these points are included in the solution set.
4. Shade the region between -5 and 5 to represent all the values of x that satisfy the inequality.
The solution set is:
{x:−5≤x≤5}
And the graph will show a solid line segment between -5 and 5, inclusive.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The solution to the inequality |2x-1| lt 6 is
Ax<−52 or x>72B−52<x<72Cx<−72 or x>52D−72<x<52 - Question 2 - Select One
If
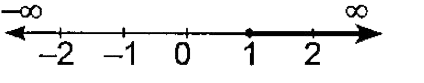 represents solution of a linear inequation in x on a number line, then the solution set in set-builder form is: A{x:x>1,x∈R}B{x:x≥1,x∈R}C{x:x>1,x∈W}D{x:x≥1,x∈W}
represents solution of a linear inequation in x on a number line, then the solution set in set-builder form is: A{x:x>1,x∈R}B{x:x≥1,x∈R}C{x:x>1,x∈W}D{x:x≥1,x∈W} - Question 3 - Select One
If
 represents the solution set of a linear inequation in x, then the solution set in set-builder form is: A{x:2−<x<3,x∈I}B{x:−2<x<3,x∈W}C{x:−2<x≤3,x∈W}D{x:−2≤x≤3,x∈I}
represents the solution set of a linear inequation in x, then the solution set in set-builder form is: A{x:2−<x<3,x∈I}B{x:−2<x<3,x∈W}C{x:−2<x≤3,x∈W}D{x:−2≤x≤3,x∈I}
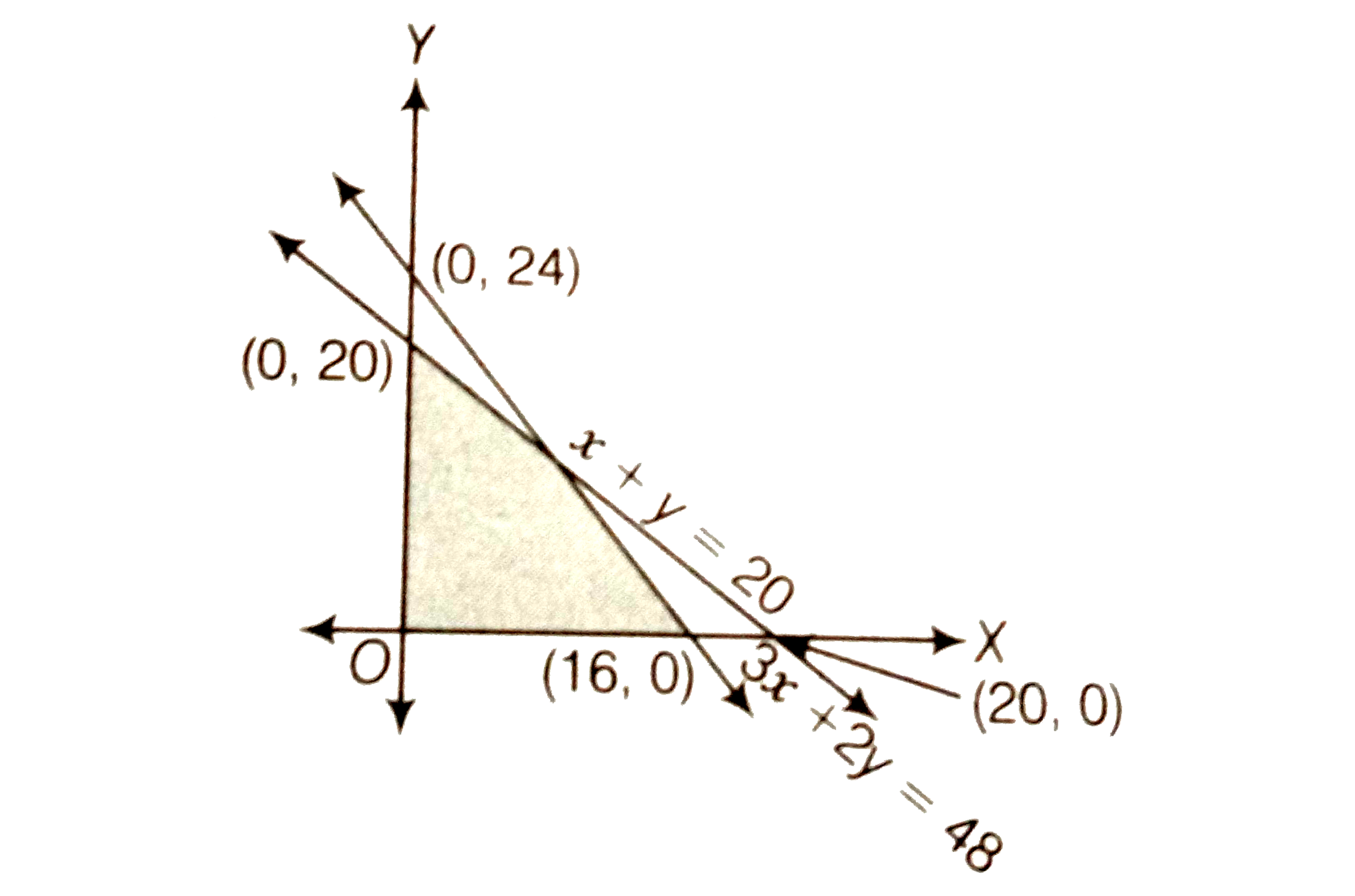
Find the linear inequalities for which the shaded region in the given figure is the solution set.
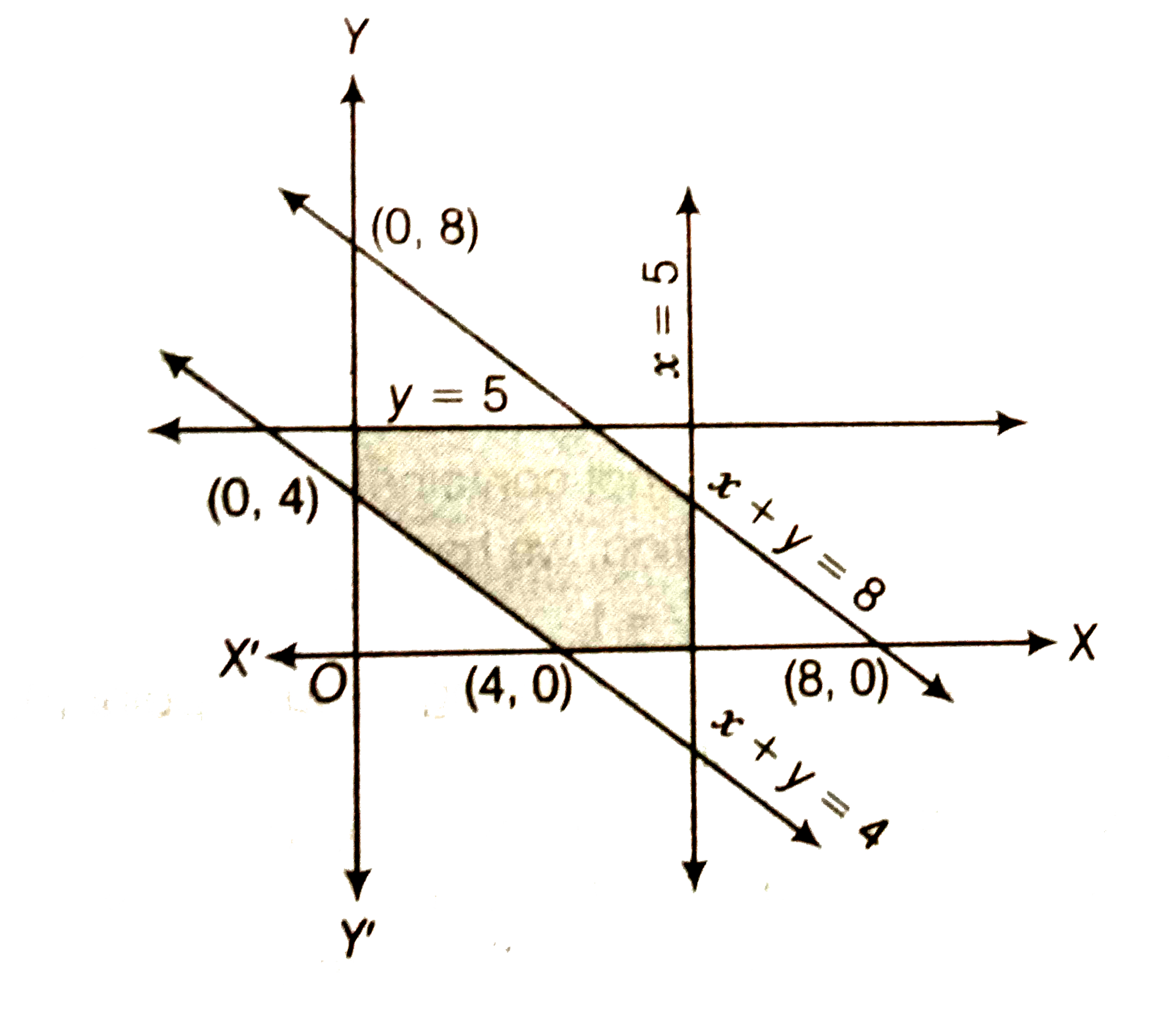 View Solution
View SolutionSolve the following inequality and represent the solution set on the real number line 2x−5≤5;x+4<11,where x∈I, I is a set of integers.
View SolutionIf
 represents the solution set of a linear inequation in x, then the solution set in set-builder form is: View Solution
represents the solution set of a linear inequation in x, then the solution set in set-builder form is: View SolutionIf
 is the solution set of a linear inequation in x, then the solution set of x in set-builder form is: View Solution
is the solution set of a linear inequation in x, then the solution set of x in set-builder form is: View SolutionIf
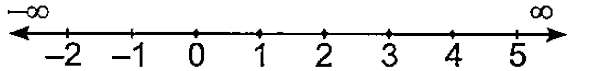 represents solution set of a linear inequation in y, then which of the following cannot be a solution set of y? View Solution
represents solution set of a linear inequation in y, then which of the following cannot be a solution set of y? View Solution