Find two numbers whose arithmetic mean is 34 and the geometric mean is 16.
To find two numbers whose arithmetic mean is 34 and geometric mean is 16, we can follow these steps:
Step 1: Set up the equations
Let the two numbers be a and b.
From the problem, we know:
1. The arithmetic mean (AM) is given by:
a+b2=34
Multiplying both sides by 2, we get:
a+b=68(Equation 1)
2. The geometric mean (GM) is given by:
√ab=16
Squaring both sides, we find:
ab=256(Equation 2)
Step 2: Use the equations to find a and b
We can express a and b in terms of each other using the equations we have.
From Equation 1:
b=68−a
Now, substitute b into Equation 2:
a(68−a)=256
Expanding this gives:
68a−a2=256
Rearranging the equation, we have:
a2−68a+256=0
Step 3: Solve the quadratic equation
We can use the quadratic formula to solve for a:
a=−b±√b2−4ac2a
Here, a=1, b=−68, and c=256.
Calculating the discriminant:
b2−4ac=(−68)2−4×1×256=4624−1024=3600
Now substituting into the quadratic formula:
a=68±√36002
Calculating √3600=60:
a=68±602
This gives us two possible values for a:
1. a=1282=64
2. a=82=4
Step 4: Find b
Using b=68−a:
1. If a=64:
b=68−64=4
2. If a=4:
b=68−4=64
Thus, the two numbers are 64 and 4.
Final Answer
The two numbers are 64 and 4.
---
Let the two numbers be a and b.
1. The arithmetic mean (AM) is given by:
a+b2=34
Multiplying both sides by 2, we get:
a+b=68(Equation 1)
√ab=16
Squaring both sides, we find:
ab=256(Equation 2)
We can express a and b in terms of each other using the equations we have.
b=68−a
a(68−a)=256
Expanding this gives:
68a−a2=256
Rearranging the equation, we have:
a2−68a+256=0
We can use the quadratic formula to solve for a:
a=−b±√b2−4ac2a
Here, a=1, b=−68, and c=256.
b2−4ac=(−68)2−4×1×256=4624−1024=3600
a=68±√36002
Calculating √3600=60:
a=68±602
1. a=1282=64
2. a=82=4
Using b=68−a:
1. If a=64:
b=68−64=4
2. If a=4:
b=68−4=64
The two numbers are 64 and 4.
Topper's Solved these Questions
Similar Questions
Find two number whose arithmetic mean is 34 and the geometric mean is 16 .
View SolutionThe harmonic mean of two numbers is 4. Their arithmetic mean A and the geometric mean G satisfy the relation 2A+G2=27. Find two numbers.
View SolutionThe harmonic mean of two positive numbers a and b is 4, their arithmetic mean is A and the geometric mean is G. If 2A+G2=27,a+b=α and |a−b|=β, then the value of αβ is equal to
View SolutionFind the arithmetic mean of 4 and 12.
View SolutionFind the arithmetic mean of:
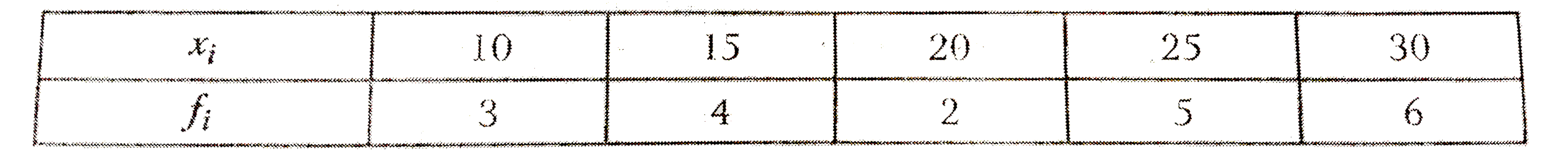
View SolutionLet two numbers have arithmatic mean 9 and geometric mean 4.Then these numbers are roots of the equation (a) x2+18x+16=0 (b) x2−18x−16=0 (c) x2+18x−16=0 (d) x2−18x+16=0
View SolutionFind the sum of 12 numbers whose mean is 11.
View SolutionFind the geometric mean of 12 and 27.
View SolutionFind the geometric mean of 6 and 24 .
View SolutionFind the single arithmetic mean between: 7and31
View Solution
