over the towers of a bridge a cable is hung in the form of a parabola, have their tops 30 meters above the road way are 200 meters apart. If the cable is 5 meters above the road way at the centre of the bridge, then the length of the vertical supporting cable 30 meters from the centre is
To solve the problem step-by-step, we will follow the given information about the parabolic cable and find the length of the vertical supporting cable 30 meters from the center of the bridge.
Step 1: Understand the problem and set up the coordinate system
- The two towers of the bridge are 200 meters apart, so we can place the center of the bridge at the origin (0, 0).
- The height of the towers is 30 meters above the roadway, and the lowest point of the cable (the vertex of the parabola) is 5 meters above the roadway.
Step 2: Determine the coordinates of key points
- The coordinates of the left tower (200 meters apart) will be (-100, 30) and the right tower will be (100, 30).
- The vertex of the parabola, which is the lowest point of the cable, is at (0, 5).
Step 3: Find the equation of the parabola
- The general form of a parabola that opens upwards is given by the equation x2=4ay.
- The vertex form of the parabola is at (0, 5), so we can express the equation as:
x2=4a(y−5)
- We know that the points (-100, 30) and (100, 30) lie on this parabola. Let's use one of these points to find a.
Step 4: Substitute the coordinates of the tower into the equation
- Using the point (100, 30):
1002=4a(30−5)
10000=4a(25)
10000=100a
a=100
Step 5: Write the equation of the parabola
- Now that we have a, we can write the equation of the parabola:
x2=400(y−5)
or equivalently,
x2=400y−2000
Step 6: Find the height of the cable at 30 meters from the center
- We need to find the height of the cable when x=30 meters from the center:
302=400y−2000
900=400y−2000
400y=900+2000
400y=2900
y=2900400=7.25
Step 7: Calculate the length of the vertical supporting cable
- The height of the cable at this point is 7.25 meters above the roadway. Since the roadway is at 0 meters, the vertical supporting cable length at this point is:
Length of supporting cable=7.25−5=2.25 meters
Step 8: Total length of the cable
- The total length of the cable from the roadway to the height at this point is:
Total length=5+2.25=7.25 meters
Final Answer
The length of the vertical supporting cable 30 meters from the center is 2.25 meters.
- The two towers of the bridge are 200 meters apart, so we can place the center of the bridge at the origin (0, 0).
- The height of the towers is 30 meters above the roadway, and the lowest point of the cable (the vertex of the parabola) is 5 meters above the roadway.
- The coordinates of the left tower (200 meters apart) will be (-100, 30) and the right tower will be (100, 30).
- The vertex of the parabola, which is the lowest point of the cable, is at (0, 5).
- The general form of a parabola that opens upwards is given by the equation x2=4ay.
- The vertex form of the parabola is at (0, 5), so we can express the equation as:
x2=4a(y−5)
- We know that the points (-100, 30) and (100, 30) lie on this parabola. Let's use one of these points to find a.
- Using the point (100, 30):
1002=4a(30−5)
10000=4a(25)
10000=100a
a=100
- Now that we have a, we can write the equation of the parabola:
x2=400(y−5)
or equivalently,
x2=400y−2000
- We need to find the height of the cable when x=30 meters from the center:
302=400y−2000
900=400y−2000
400y=900+2000
400y=2900
y=2900400=7.25
- The height of the cable at this point is 7.25 meters above the roadway. Since the roadway is at 0 meters, the vertical supporting cable length at this point is:
Length of supporting cable=7.25−5=2.25 meters
- The total length of the cable from the roadway to the height at this point is:
Total length=5+2.25=7.25 meters
The length of the vertical supporting cable 30 meters from the center is 2.25 meters.
Topper's Solved these Questions
Similar Questions
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
View SolutionIf from the top of a tower 80 meters high the angles of depression of the top and bottom of a house are 30∘and45∘ respectively, then the height of the house is
View Solution
Knowledge Check
A ladder rests against the side of a wall and reaches a point that is h meters above the ground. The angle formed by the ladder and the ground is θ∘. A point on the ladder is k meters from the wall.What is the vertical distance, in meters, from this point on the ladder to the ground?
A(h−k)tanθ∘B(h−k)cosθ∘Ch−ksinθ∘Dh−ktanθ∘y=−5t2+2t+20
x=2t
A cannonball is shot out of a cannon at a 45∘ angle with an approxiate speed of 283m/s. The cannon from which the ball was fired sits on the edges of a cliff, and its height above the ground is 20 meters. The equations given above represent the cannonball's height above the ground(y) and its horizontal distance (x) from the face of the cliff, t seconds after the ball was fired, where t≥0. How many seconds after the ball was fired does its vertical height above the ground equal its horizontal distance from the cliff?A1B2C3D4
If the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
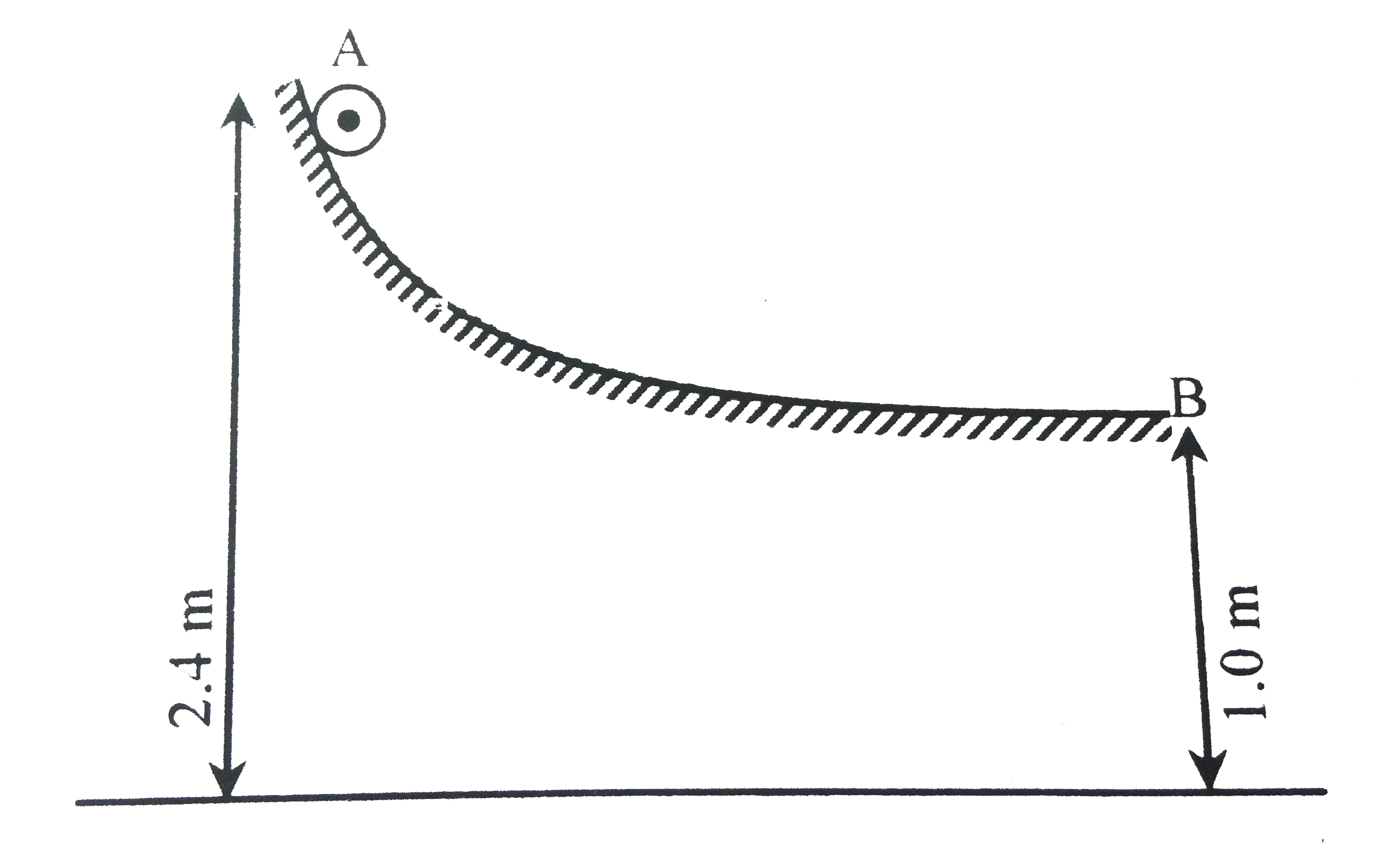 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionThe cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of which is at 18m apart from the middle point of cable.
View SolutionA tower subtends an angle of 30∘ at a point on the same level as the foot of the tower. At a second point h meter above the first, the depression of the foot of the tower is 60∘. The horizontal distance of the tower from the point is
View SolutionIf the angle of elevation of a cloud from a point P which is 25 m above a lake be 30∘ and the angle of depression of reflection of the cloud in the lake from P be 60∘, then the height of the cloud (in meters) from the surface of the lake is
View SolutionThe cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find t
View Solution
