An open tank is to be constructed with square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead will be least, if depth is made half of width.
To solve the problem of minimizing the expenses of lining an open tank with a square base and vertical sides, we will follow these steps:
Step 1: Define the Variables
Let:
- x = length of each side of the square base
- y = depth of the tank
Step 2: Write the Volume Equation
The volume V of the tank is given by:
V=length×breadth×depth=x×x×y=x2y
This is our first equation.
Step 3: Write the Surface Area Equation
The surface area S of the open tank (which has no top) is given by:
S=Area of base+Area of four sides=x2+4(x⋅y2)=x2+2xy
Step 4: Express Depth in Terms of Volume and Base Length
From the volume equation, we can express y:
y=Vx2
Step 5: Substitute y into the Surface Area Equation
Substituting y into the surface area equation gives:
S=x2+2x(Vx2)=x2+2Vx
Step 6: Differentiate the Surface Area with Respect to x
To find the minimum surface area, we differentiate S with respect to x:
dSdx=2x−2Vx2
Step 7: Set the Derivative Equal to Zero
Setting the derivative equal to zero to find critical points:
2x−2Vx2=0
This simplifies to:
2x3=2V⇒x3=V⇒x=V1/3
Step 8: Find y in Terms of x
Now substituting back to find y:
y=Vx2=V(V1/3)2=VV2/3=V1/3
Step 9: Relate Depth to Width
From the relationship we derived, we can express y in terms of x:
y=x2
This means that the depth y is half of the width x.
Step 10: Verify Minimum Condition
To confirm that this critical point is indeed a minimum, we can check the second derivative:
d2Sdx2=2+4Vx3
Since V and x are positive, d2Sdx2>0, indicating that the surface area is minimized.
Conclusion
Thus, the expenses of lining the tank will be least when the depth y is half of the width x.
---
Let:
- x = length of each side of the square base
- y = depth of the tank
The volume V of the tank is given by:
V=length×breadth×depth=x×x×y=x2y
This is our first equation.
The surface area S of the open tank (which has no top) is given by:
S=Area of base+Area of four sides=x2+4(x⋅y2)=x2+2xy
From the volume equation, we can express y:
y=Vx2
Substituting y into the surface area equation gives:
S=x2+2x(Vx2)=x2+2Vx
To find the minimum surface area, we differentiate S with respect to x:
dSdx=2x−2Vx2
Setting the derivative equal to zero to find critical points:
2x−2Vx2=0
This simplifies to:
2x3=2V⇒x3=V⇒x=V1/3
Now substituting back to find y:
y=Vx2=V(V1/3)2=VV2/3=V1/3
From the relationship we derived, we can express y in terms of x:
y=x2
This means that the depth y is half of the width x.
To confirm that this critical point is indeed a minimum, we can check the second derivative:
d2Sdx2=2+4Vx3
Since V and x are positive, d2Sdx2>0, indicating that the surface area is minimized.
Thus, the expenses of lining the tank will be least when the depth y is half of the width x.
Topper's Solved these Questions
Similar Questions
An open tank with a square base and vertical sides is to be constructed form a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when depth of tank is half its width. If the cost is to be borne by nearby settled lower income families, for whom water will be provided, what kind of value is hidden in the question
View SolutionA metal box with a square base and vertical sides is to contain 1024 cm3 of water, the material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box.
View SolutionAn open box with a square base is to be made out of a given quantity of card board of area c2 square units. Show that the maximum volume of the box is c36√3 cubic units.
View SolutionAn open box with a square base is to be made out of a given quantity of card board of area c2 square units. Show that the maximum volume of the box is c36√3 cubic units.
View SolutionOR An open box with a square base is to be made out of a given quantity of cardboard of area c2 square units. Show that the maximum volume of the box is c36 √3 cubic units.
View SolutionA liquid having density 6000kg/m3 stands to a height of 4m in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of 3atm. The horizontal outlet pipe has a cross-sectional area of 6cm2 and 3cm2 at larger and smaller sections. Atmospheric pressure =1atm,g=10m/s21atm=105N/m2.
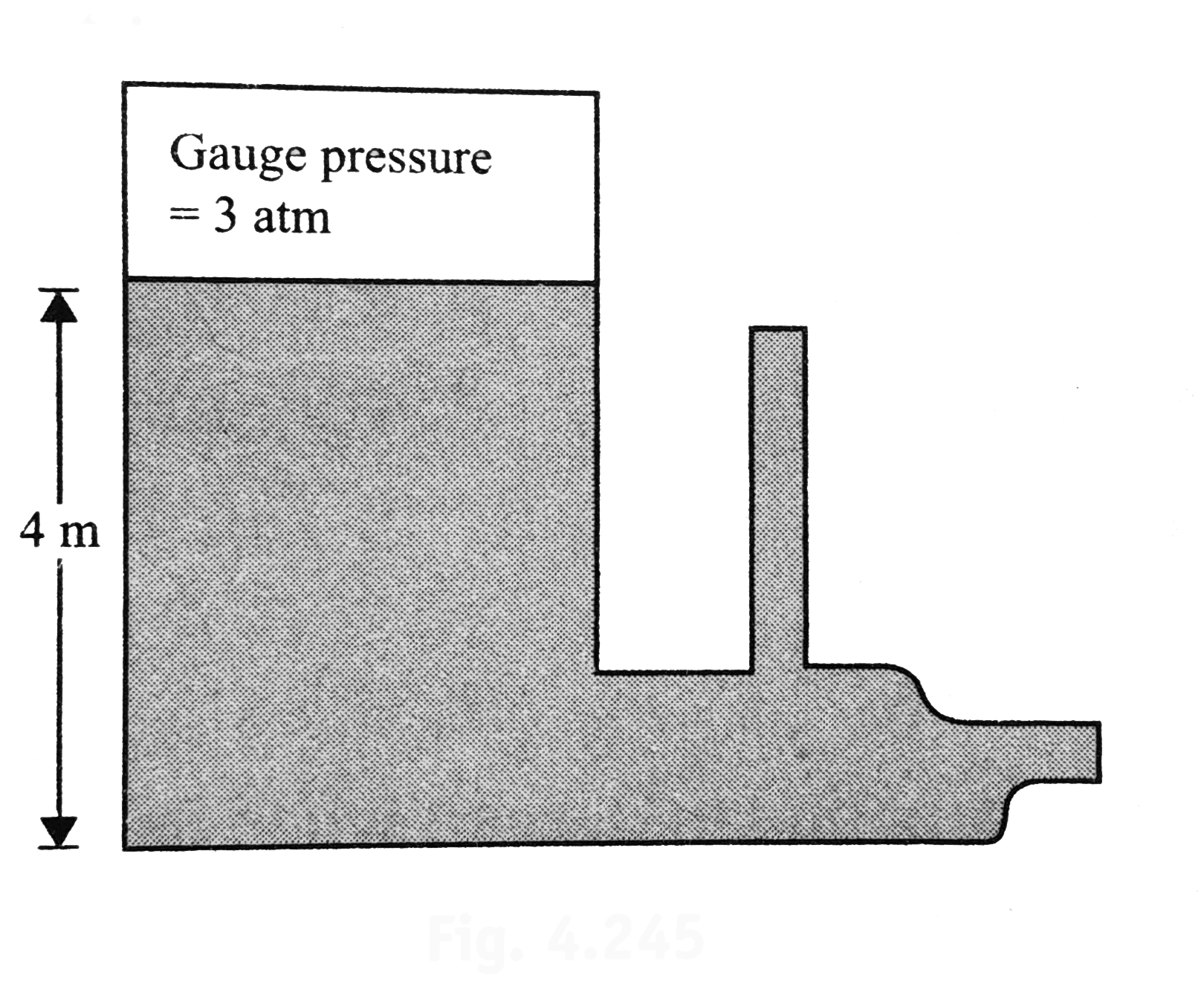
Assume that depth of water in the tank remains constant due to s very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The height at which liquid will stand in the open end of the pipe is
View SolutionA tank with rectangular base and rectangular sides open at the top is to be constructed so that its depth is 3 m and volume is 75 m3. If building of tank costs Rs. 100 per square metre for the base and Rs. 50 per square metre for the sides, find the cost of least expensive tank.
View SolutionA tank with rectangular base and rectangular sides open at the top is to be constructed so that its depth is 3 m and volume is 75 m3. If building of tank costs Rs. 100 per square metre for the base and Rs. 50 per square metres for the sides, find the cost of least expensive tank.
View SolutionA tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2m and volume is 8m3 . If building of tank costs Rs.70 per sq. metre for the base and Rs.45 per sq. metre for sides, what is the cost of least expensive tank?
View SolutionWater is drained from a vertical cylindrical tank by opening a valve at the base of the tank. It is known that the rate at which the water level drops is proportional to the square root of water depth y, where the constant of proportionality k>0 depends on the acceleration due to gravity and the geometry of the hole. If t is measured in minutes and k=115, then the time to drain the tank if the water is 4 m deep to start with is (a) 30 min (b) 45 min (c) 60 min (d) 80 min
View Solution