A liquid having density 6000kg/m3 stands to a height of 4m in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of 3atm. The horizontal outlet pipe has a cross-sectional area of 6cm2 and 3cm2 at larger and smaller sections. Atmospheric pressure =1atm,g=10m/s21atm=105N/m2.
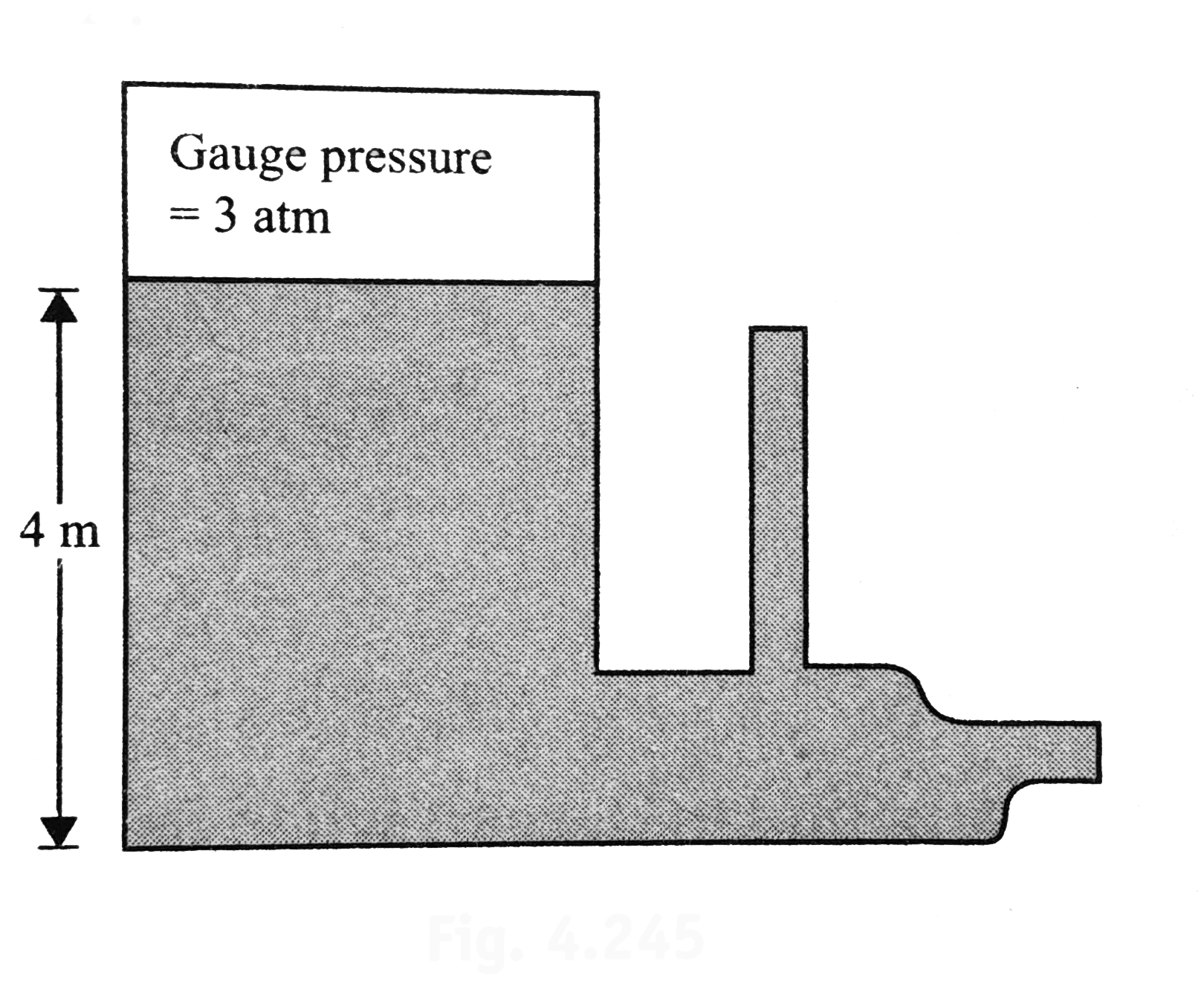
Assume that depth of water in the tank remains constant due to s very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The height at which liquid will stand in the open end of the pipe is
4m
3.5m
4.5m
5.6m
The correct Answer is:C
Let atmospheric pressure be p0. Then absolute pressure of air is p+p0=4atm
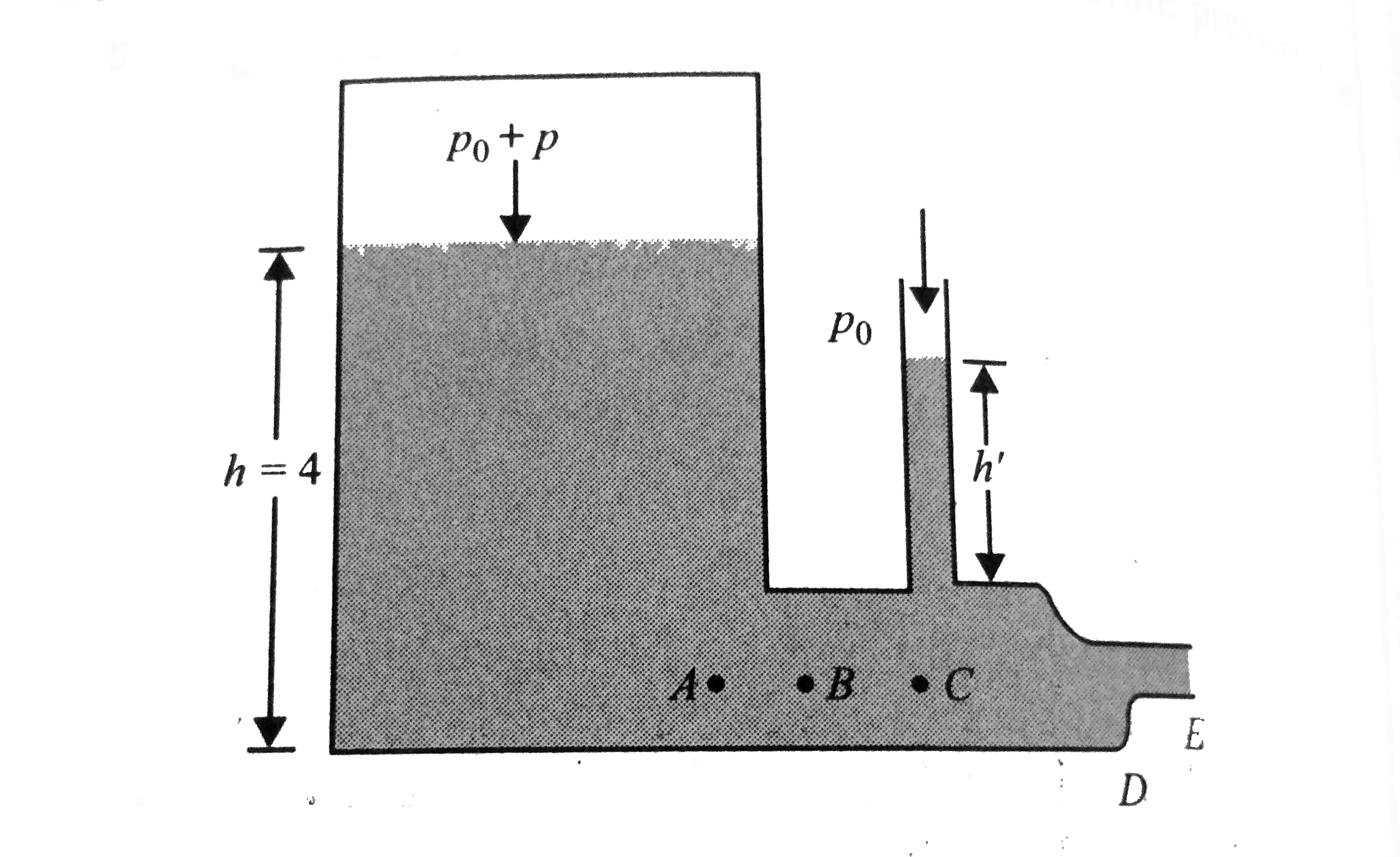
Pressure at A,pA=p+p0+ρgh
From equation of continuity and Bernoulli's theorem,
pB=pC
Applying Bernoull's theorem at A and E, we have
p+p0+ρgh=pc+pv2C2=p0+pv2E2
where vC and vE are the velocities of flow of liquid at C and E, respectively.
From hydrostastics pc=p0+ρgh'
From continuity equation ACvC=AEvE
Where AC=6cm2 and AE=3cm2
Solving above equation, we get vE=13.4m/s
vC=6.7m/s
h'=4.5m
Discharge rate
Q=AEvE=3×10−4×13.4m3/s
When a hole has been created at the top of the vessel, gange pressure drops to zero, i.e,, in above equation put p=0 and get h'.
∴h'=3m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE13videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A liquid having density 6000kg/m3 stands to a height of 4m in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of 3atm. The horizontal outlet pipe has a cross-sectional area of 6cm2 and 3cm2 at larger and smaller sections. Atmospheric pressure =1atm,g=10m/s21atm=105N/m2.

Assume that depth of water in the tank remains constant due to s very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The discharge rate from the outlet isView Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isView SolutionIf the gauge pressure, at the bottom of a water tank is 2.7 kPa, what is the height of the water [Take g = 10 m s−2]
Hint : Gauge Pressure = absolute pressure - atmospheric pressure = pghView SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).View SolutionA brass rod of cross-sectional area 1cm2 and length 0.2 m is compressed lengthwise by a weight of 5 kg. if young's modulus of elasticity of brass is 1×1011N/m2 and g=10m/sec2 then increase in the energy of the rod will be
View SolutionThe volume of a solid is 6×10−3m3 under 2 atm pressure. Find the change in volume when subjected to a pressure of 102 atm. Bulk modulus of the material =1011Nm−2.
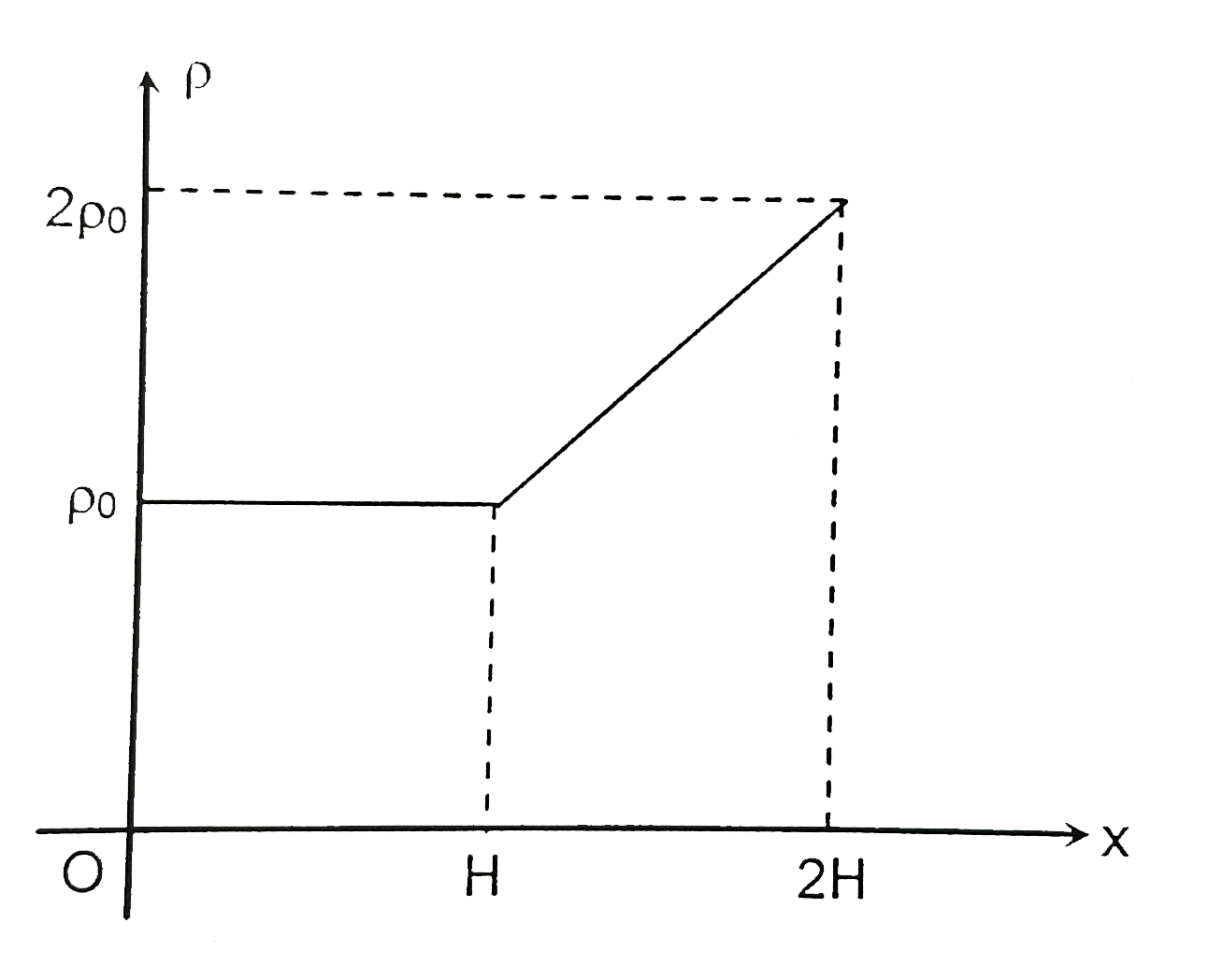
View SolutionA large cylindrical container with open top contains a liquid upto height (2H=8m) and whose density varies as shown in the figure. Atmospheric pressure is 1 atm (=105N/m2)
Find the pressure at botom of cylindrical container in atm.
(given ρ0=103Kg/m2, and g=10m/s2)
 View Solution
View SolutionAt sea level, the atmospheric pressure is 1.04×105 Pa. Assuming g=10m s−2 and density of air to be uniform and equal to 1.3kg m−3, find the height of the atmosphere.
View SolutionA horizontal pipe of varying cross-sectional area carries water flowing at a constant rate. The pressure at sections (1) and (2) are 50cm and 20cm of Hg. If the velocity of section (1) is 5m/s, what is the velocity of section (2). Also determine the ratio of areas at sections (1) and (2) (as shown in Fig.
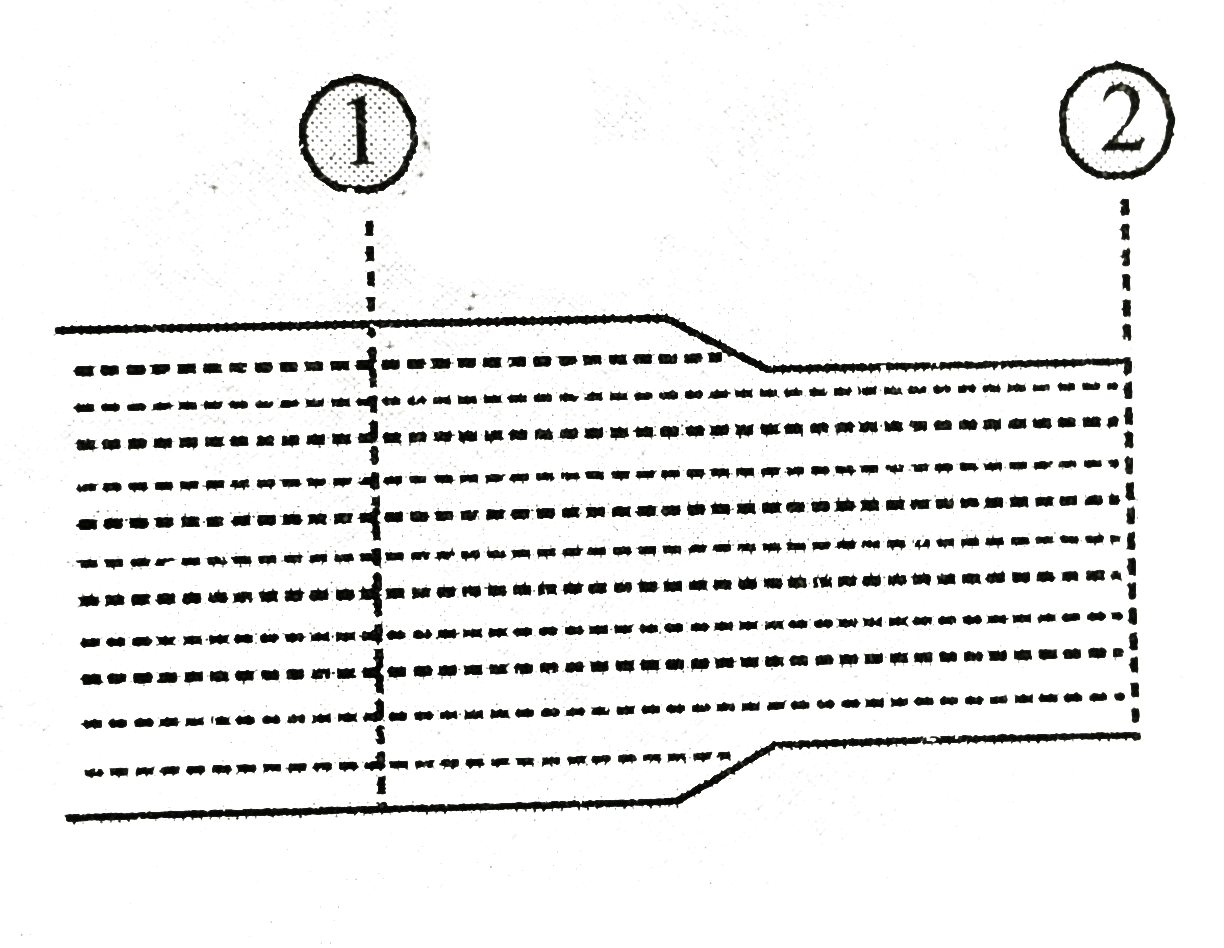 View Solution
View SolutionA pipe of varying area of cross-section is held such that its axis is horizontal. At two cross sections A and B, its radii are 8 cm and 4 cm. If velocity of water at A through the pipe is 16 cm s−1 and pressure at A is 106 dyne/cm2 , find the pressure at cross-section B.
View Solution

