Solve the following initial value problem: drdt= −rt, r(0)=r0
Step by step video & image solution for Solve the following initial value problem: (d r)/(dt)=\ -r t ,\ r(0) = r_0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If S be the surface area of V be the volume of a sphere of radius r. Then dvdt=rkdsdt. Value of k is
A12B14C2D4
Differentiate the following w.r.t.x
View SolutionA soap bubble of radius 'r' and surface tension 'T' is given a potential of 'V' volt. If the new radiys 'R' of the bubble is related to its initial radius by equation.
P0[R3−r3]+[λT[R2−r2]−ε0V2R/2=0, where P0 is the atmospheric pressure. Then find λ
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
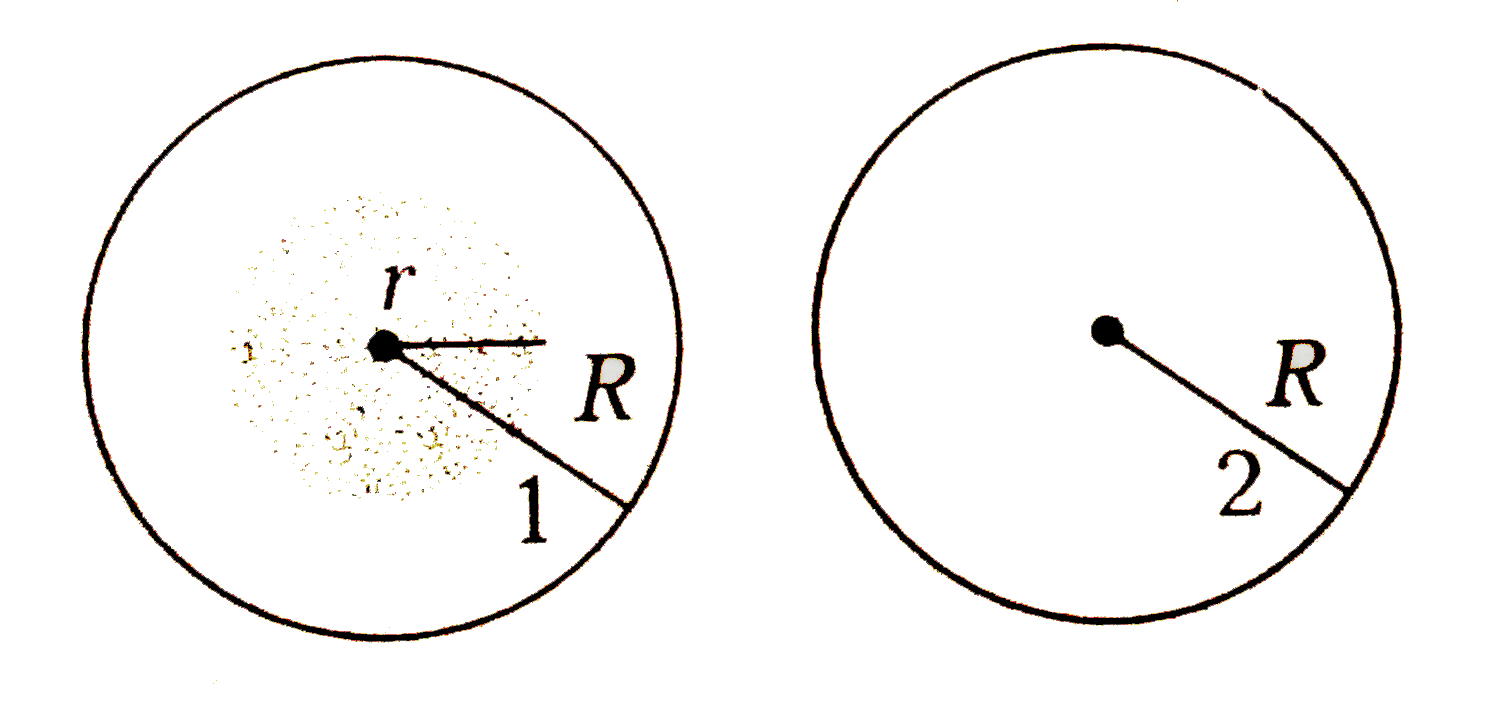
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View SolutionThe inversion of a sugar follows first order rate equation which can be followed by noting the change in the rotation of the plane of polarization of light in the polarimeter. If r∞,rf and r0 are the rotations at t=∞,t=t, and t=0, then the first order reaction can be written as
(a)k=1tlog.r1−r∞ro−r∞
(b) k=1tln.r0−r∞rt−ro
(c) k=1tln.r∞−ror∞−rt
(d)k=1tln.r∞−rtr∞−r0
View SolutionA soap bubble of radius 'r' and surface tension 'T' is given a potential of 'V' volt. If the new radiys 'R' of the bubble is related to its initial radius by equation.
P0[R3−r3]+[λT[R2−r2]−ε0V2R/2=0, where P0 is the atmospheric pressure. Then find λ
View SolutionCurrent density in a cylindrical wire of radius R is given as J=⎧⎪⎨⎪⎩J0(xR−1) for 0≤x<R2J0xR for R2≤x≤R.
If the current flowing in the wire is k12πJ0R2, find the value of k.
View SolutionFind the value of ∞∑r=0tan−1(11+r+r2)
View Solution
