The inversion of a sugar follows first order rate equation which can be followed by noting the change in the rotation of the plane of polarization of light in the polarimeter. If r∞,rf and r0 are the rotations at t=∞,t=t, and t=0, then the first order reaction can be written as
(a)k=1tlog.r1−r∞ro−r∞
(b) k=1tln.r0−r∞rt−ro
(c) k=1tln.r∞−ror∞−rt
(d)k=1tln.r∞−rtr∞−r0
k=1tlog.r1−r∞ro−r∞
k=1tln.r0−r∞rt−ro
k=1tln.r∞−ror∞−rt
k=1tln.r∞−rtr∞−r0
The correct Answer is:B
To solve the problem regarding the first-order reaction of sugar inversion and its relationship with the rotation of polarized light, we can follow these steps:
1. Understand the Reaction:
The inversion of sugar (sucrose) into glucose and fructose can be represented as:
Cane SugarH2O−−→Glucose+Fructose
This reaction follows first-order kinetics.
2. Define the Variables:
- r0: Rotation at time t=0 (initial rotation).
- rt: Rotation at time t.
- r∞: Rotation at time t=∞ (final rotation when the reaction is complete).
3. Determine the Change in Rotation:
The change in rotation can be defined as:
- The amount of sugar that has reacted at time t can be represented as x.
- Therefore, the rotation at any time t can be expressed in terms of the initial and final rotations:
x=r0−rt
At t=∞:
x=r0−r∞
4. Apply the First-Order Rate Law:
For a first-order reaction, the rate constant k can be expressed as:
k=2.303tlog((A)0(A))
where (A)0 is the initial concentration and (A) is the concentration at time t.
5. Relate Concentrations to Rotations:
Using the relationship between the concentrations and the rotations:
(A)0=r0−r∞and(A)=r0−rt
We can substitute these into the rate equation:
k=2.303tlog(r0−r∞r0−rt)
6. Convert Logarithm to Natural Log:
Since the options are given in natural logarithm (ln), we can use the conversion:
logx=lnx2.303
Thus, we can rewrite the equation as:
k=1tln(r0−r∞r0−rt)
7. Identify the Correct Option:
After analyzing the options provided:
- The correct expression matches option (b):
k=1tln(r0−r∞rt−r∞)
Conclusion:
The correct answer is:
(b) k=1tln(r0−r∞rt−r∞)
The inversion of sugar (sucrose) into glucose and fructose can be represented as:
Cane SugarH2O−−→Glucose+Fructose
This reaction follows first-order kinetics.
- r0: Rotation at time t=0 (initial rotation).
- rt: Rotation at time t.
- r∞: Rotation at time t=∞ (final rotation when the reaction is complete).
The change in rotation can be defined as:
- The amount of sugar that has reacted at time t can be represented as x.
- Therefore, the rotation at any time t can be expressed in terms of the initial and final rotations:
x=r0−rt
At t=∞:
x=r0−r∞
For a first-order reaction, the rate constant k can be expressed as:
k=2.303tlog((A)0(A))
where (A)0 is the initial concentration and (A) is the concentration at time t.
Using the relationship between the concentrations and the rotations:
(A)0=r0−r∞and(A)=r0−rt
We can substitute these into the rate equation:
k=2.303tlog(r0−r∞r0−rt)
Since the options are given in natural logarithm (ln), we can use the conversion:
logx=lnx2.303
Thus, we can rewrite the equation as:
k=1tln(r0−r∞r0−rt)
After analyzing the options provided:
- The correct expression matches option (b):
k=1tln(r0−r∞rt−r∞)
The correct answer is:
(b) k=1tln(r0−r∞rt−r∞)
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Assertion-Reasoning
22 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Integer
15 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
33 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
If ∞∑r=1Crr!=1 then C =
View SolutionA satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √rpra respectively. The angular momentum of the satellite is: (A) 2mπ(rB+rp)√rarpT (B) mπ(ra+rp)√rarp2T (C) mπ(ra+rp)√rarp4T (D) mπ(ra+rp)√rarpT
View Solution
Knowledge Check
If r>0andtt=6.25rt+2, then r=
A25B49C58D34
The domain of definition of the function f(x)=log|x| is a.R b. (−∞,0) c. (0,∞) d. R−{0}
View SolutionIf αandβ are the roots of the quadratic equation 4x2+2x−1=0 then the value of ∞∑r=1(ar+βr) is :
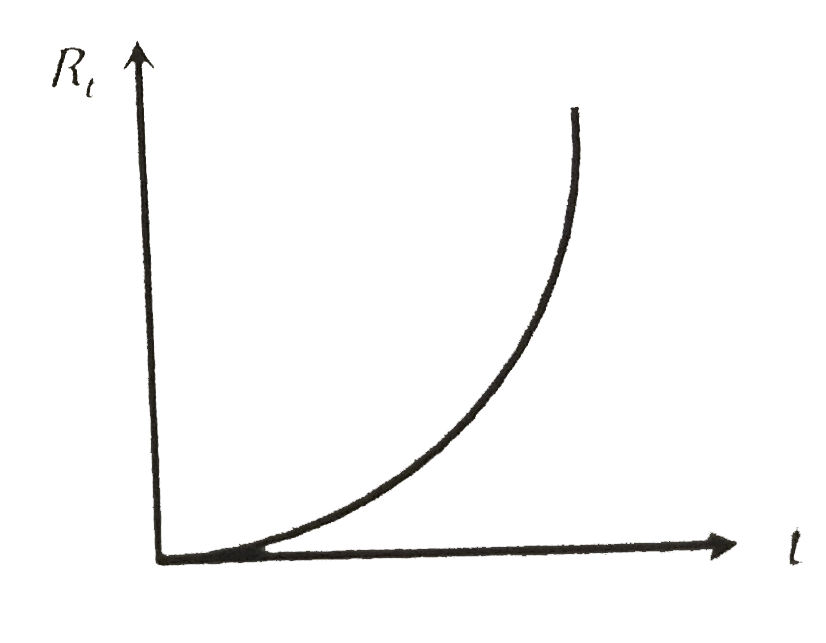
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
View SolutionThe radioactivity of a sample is R1 at a time T1 and R2 at time T2. If the half-life of the specimen is T, the number of atoms that have disintegrated in the time (T2−T1) is proporational to
View SolutionSolve the following initial value problem: drdt= −rt, r(0)=r0
View SolutionThe value of ∞∑r=18r4r4+1 is equal to :
View Solution∞∑r=1(4r+5)5−rr(5r+5)
View Solution
