A girl walks 4 km towards west, then she walks 3 km in a direction 30oeast of north and stops. Determine the girls displacement from her initial point of departure.
To determine the girl's displacement from her initial point of departure, we will break down her movements into vector components and then sum them up.
Step 1: Represent the first movement
The girl walks 4 km towards the west. In vector notation, we can represent this movement as:
→A=−4^i km
where ^i is the unit vector in the east-west direction (with west being negative).
Step 2: Represent the second movement
Next, she walks 3 km in a direction that is 30 degrees east of north. We need to break this movement into its northward and eastward components.
Using trigonometry:
- The eastward (x-direction) component is given by:
East component=3sin(30∘)=3⋅12=1.5 km
- The northward (y-direction) component is given by:
North component=3cos(30∘)=3⋅√32=3√32 km
Thus, we can represent this second movement as:
→B=1.5^i+3√32^j km
Step 3: Sum the vectors
Now, we add the two vectors →A and →B to find the resultant displacement vector →R:
→R=→A+→B=(−4^i)+(1.5^i+3√32^j)
→R=(−4+1.5)^i+3√32^j
→R=−2.5^i+3√32^j km
Step 4: Calculate the magnitude of the displacement
The magnitude of the displacement vector →R can be calculated using the Pythagorean theorem:
|→R|=
⎷(−2.5)2+(3√32)2
Calculating each component:
(−2.5)2=6.25
(3√32)2=9⋅34=274=6.75
Now, summing these:
|→R|=√6.25+6.75=√13 km
Step 5: Determine the direction of the displacement
To find the direction of the displacement, we can calculate the angle θ with respect to the west direction using the tangent function:
tan(θ)=North componentWest component=3√322.5
Calculating θ:
θ=tan−1⎛⎜⎝3√322.5⎞⎟⎠
Final Result
The girl's displacement from her initial point of departure is:
|→R|=√13 km at an angle θ north of west.
---
The girl walks 4 km towards the west. In vector notation, we can represent this movement as:
→A=−4^i km
where ^i is the unit vector in the east-west direction (with west being negative).
Next, she walks 3 km in a direction that is 30 degrees east of north. We need to break this movement into its northward and eastward components.
- The eastward (x-direction) component is given by:
East component=3sin(30∘)=3⋅12=1.5 km
- The northward (y-direction) component is given by:
North component=3cos(30∘)=3⋅√32=3√32 km
→B=1.5^i+3√32^j km
Now, we add the two vectors →A and →B to find the resultant displacement vector →R:
→R=→A+→B=(−4^i)+(1.5^i+3√32^j)
→R=(−4+1.5)^i+3√32^j
→R=−2.5^i+3√32^j km
The magnitude of the displacement vector →R can be calculated using the Pythagorean theorem:
|→R|=
⎷(−2.5)2+(3√32)2
Calculating each component:
(−2.5)2=6.25
(3√32)2=9⋅34=274=6.75
Now, summing these:
|→R|=√6.25+6.75=√13 km
To find the direction of the displacement, we can calculate the angle θ with respect to the west direction using the tangent function:
tan(θ)=North componentWest component=3√322.5
Calculating θ:
θ=tan−1⎛⎜⎝3√322.5⎞⎟⎠
The girl's displacement from her initial point of departure is:
|→R|=√13 km at an angle θ north of west.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A man walks 4 km towards the north in one hour and then 3 km towards the east in the next hour. His average velocity is
A3.5kmh−1B2.5kmh−1C5kmh−1D6kmh−1
A girl travels 4 km west and then 4 km north. What is the distance and displacement of the girl ?
View SolutionA car moves with speed 60km/h for 1 hour in east direction and with same speed for 30 min in south direction. The displacement of car from initial posilion is
View SolutionA man moves towards 3m north then 4 m towards east and finally 5 m towards 37∘ south of west. His displacement from origin is :-
View SolutionRepresent graphically a displacement of 40 km, 30oeast of north.
View SolutionA person moves towards East for 3 m, then towards North for 4 m and then moves vertically up by 5 m. What is his distance now from the starting point ?
View SolutionA physics professor leaves her house and walks along the sidewalk towards campus. After 5min, it starts to rain and she returns home. Her distance from her house as a function of time is shown in .
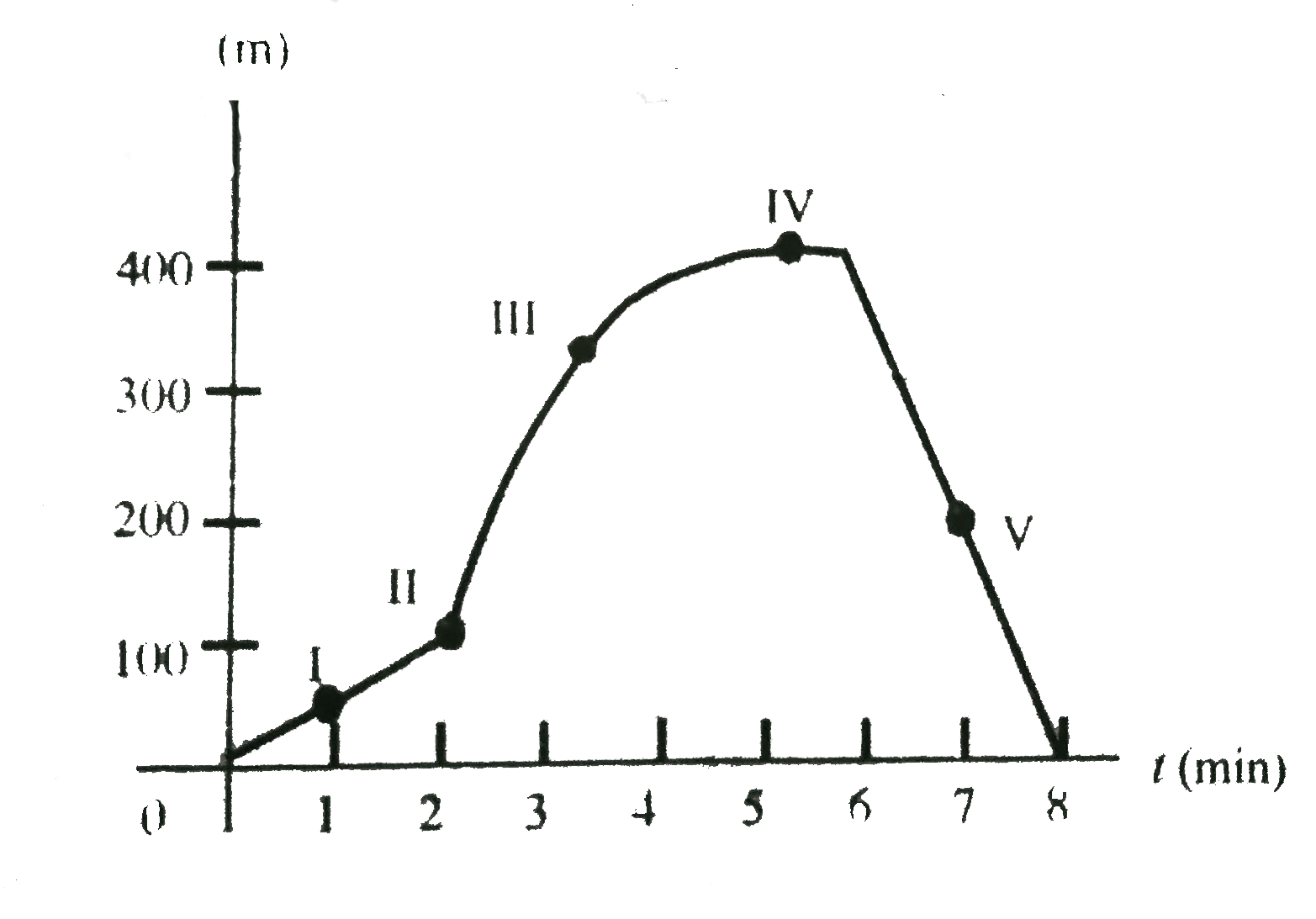 .
.
At which of the labeld points is her velocity
a. Zero
b. Constant and positive
c. Constant and negative
d. Increasing in magnitude .View SolutionA bomb is projected with speed 10 m/s at an angle 30o with the horizontal. In the mid-air bomb explodes in different fragments and they all move in different directions. At the time when all fragments reach at ground, the displacement of the center of mass of bomb from initial point will be (g = 10 m/s2)
View Solution

