Prove that the diagonals of a rectangle are perpendicular if and only if the rectangle is a square.
Step by step video & image solution for Prove that the diagonals of a rectangle are perpendicular if and only if the rectangle is a square. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove analytically that the diagonals of a rectangle are equal
View SolutionThe diagonals of a rectangle are of equal length.
View SolutionProve that the diagonals of a rectangle bisect each other and are equal.
View SolutionThe diagonals of a rectangle bisect each other
View SolutionWhat is the diagonal of the rectangle shown?
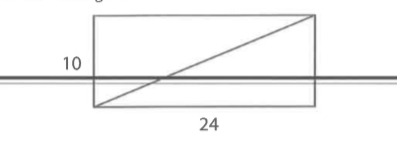
View SolutionThe diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
View SolutionWhich of the following statements are true for a rectangle? It has two pairs of equal sides. It has all its sides of equal length. Its diagonals are equal. Its diagonals bisect each other. Its diagonals are perpendicular. Its diagonals are perpendicular and bisect each other. Its diagonals are equal and bisect each other. Its diagonals are equal and perpendicular, and bisect each other. All rectangles are squares. All rhombuses are parallelograms. All squares are rhombuses and also rectangles. All squares are not parallelograms.
View SolutionThe equation of the diagonals of a rectangle are y+8x−17=0 and y−8x+7=0. If the area of the rectangle is 8squnits then find the sides of the rectangle
View SolutionGiven below are two pairs of statements. Combine these two statements using "if and only if". (i) p: If a rectangle is a square, then all its four sides are equal. q: If all the four sides of a rectangle are equal, then the rectangle is a square.
View SolutionGiven below are two pairs of statements. Combine these two statements using if and only if: p: if a rectangle is a square, then all its four sides are equal. q : if all the four sides of a rectangle are equal, then the rectangle is a square
View Solution