The optimal value of the objective function is attained at the points A)Given by intersection of inequations with the axes only B)Given by intersection of inequations with the axes only C)Given by corner points of the feasible region D)None of these
To solve the question regarding the optimal value of the objective function in linear programming, we can follow these steps:
1. Understand the Problem: The question asks where the optimal value of the objective function is attained in a linear programming problem (LPP). We have four options to consider.
2. Graphical Representation: In linear programming, we typically represent the constraints graphically. This involves plotting the inequalities on a graph to visualize the feasible region.
3. Identify the Feasible Region: The feasible region is the area on the graph where all the constraints overlap. This region represents all possible solutions that satisfy the given inequalities.
4. Locate the Corner Points: The feasible region is usually a polygon, and the points where the edges of this polygon intersect are known as corner points (or vertices).
5. Evaluate the Objective Function: To find the optimal value, we evaluate the objective function at each of the corner points. The maximum or minimum value (depending on the objective) will give us the optimal solution.
6. Conclusion: Based on the above steps, we can conclude that the optimal value of the objective function is attained at the corner points of the feasible region.
7. Select the Correct Option: Among the given options, the correct answer is:
C) Given by corner points of the feasible region.
C) Given by corner points of the feasible region.
Topper's Solved these Questions
Similar Questions
Maximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionA, B C and D are the points of intersection with the coordinate axes of the lines ax+by=ab and bx+ay=ab, then
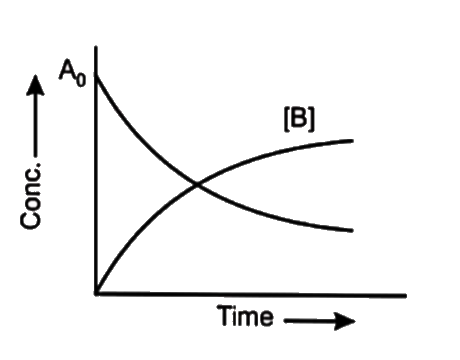
View SolutionAt the point of intersection of the two curves shown, the conc. of B is given by ……… for, A→nB:
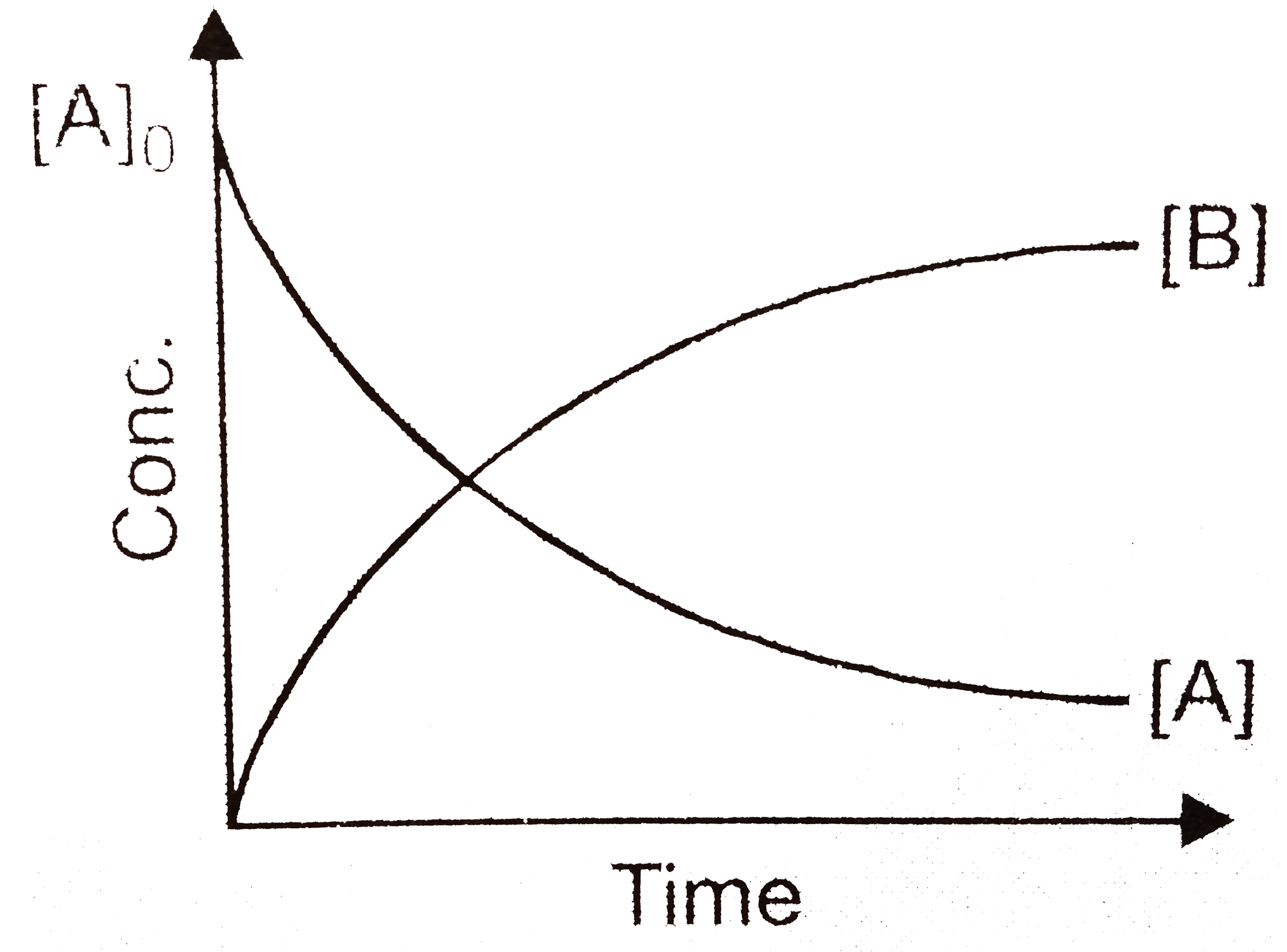
View SolutionAt the point of intersection of the two curves shown the concentration of B is given by _______for the first reaction A→nB.
View SolutionThe coordinates of the centriod of triangle ABC where A,B,C are the points of intersection of the plane 6x+3y−2z=18 with the coordinate axes are :
View SolutionObjective function of a LLP is
(A) a constraint
(B) a function to be optimized
(C) a relation between the variables
(D) none of these
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View SolutionFor a>b>c>0, the distance between (1, 1) and the point of intersection of the lines ax+by+c =0 and bx+ay+c=0 is les than 2√2. Then
View SolutionIf a circle passes through the points of intersection of the lines 2x−y+1=0 and x+λy−3=0 with the axes of reference then the value of λ is :
View Solution
