The value of objective function is maximum under linear constraints (a) At the centre of feasible region (b)At (0,0) (c)At any vertex of feasible region (d)The vertex which is maximum distance from (0,0)
Step by step video & image solution for The value of objective function is maximum under linear constraints (a) At the centre of feasible region (b)At (0,0) (c)At any vertex of feasible region (d)The vertex which is maximum distance from (0,0) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In an L.P.P. if the objective function Z=ax+by by has same maximum value on two corner points of the feasible region, then the number of points at which maximum value of Z occurs is
A0B2CfiniteDinfiniteIf the objective function for a L.P.P. is Z=5x+7y and the corner points of the bounded feasible region are (0, 0), (7, 0), (3, 4) and (0, 2), then the maximum value of Z occurs at
AA) (0, 0)BB) (7, 0)CC) (3, 4)DD) (0, 2)If the objective function for an L.P.P. is Z=3x−4y and the corner points for the bounded feasible region are (0, 0), (5, 0), (6, 5), (6, 8), (4, 10) and (0, 8), then the maximum value of Z occurs at
A(0, 0)B(0, 8)C(5, 0)D(4, 10)
In a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View SolutionThe optimal value of the objective function is attained at the points A)Given by intersection of inequations with the axes only B)Given by intersection of inequations with the axes only C)Given by corner points of the feasible region D)None of these
View SolutionIn telescope of objective diameter (2a), the radius of the central bright region (r0) is
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
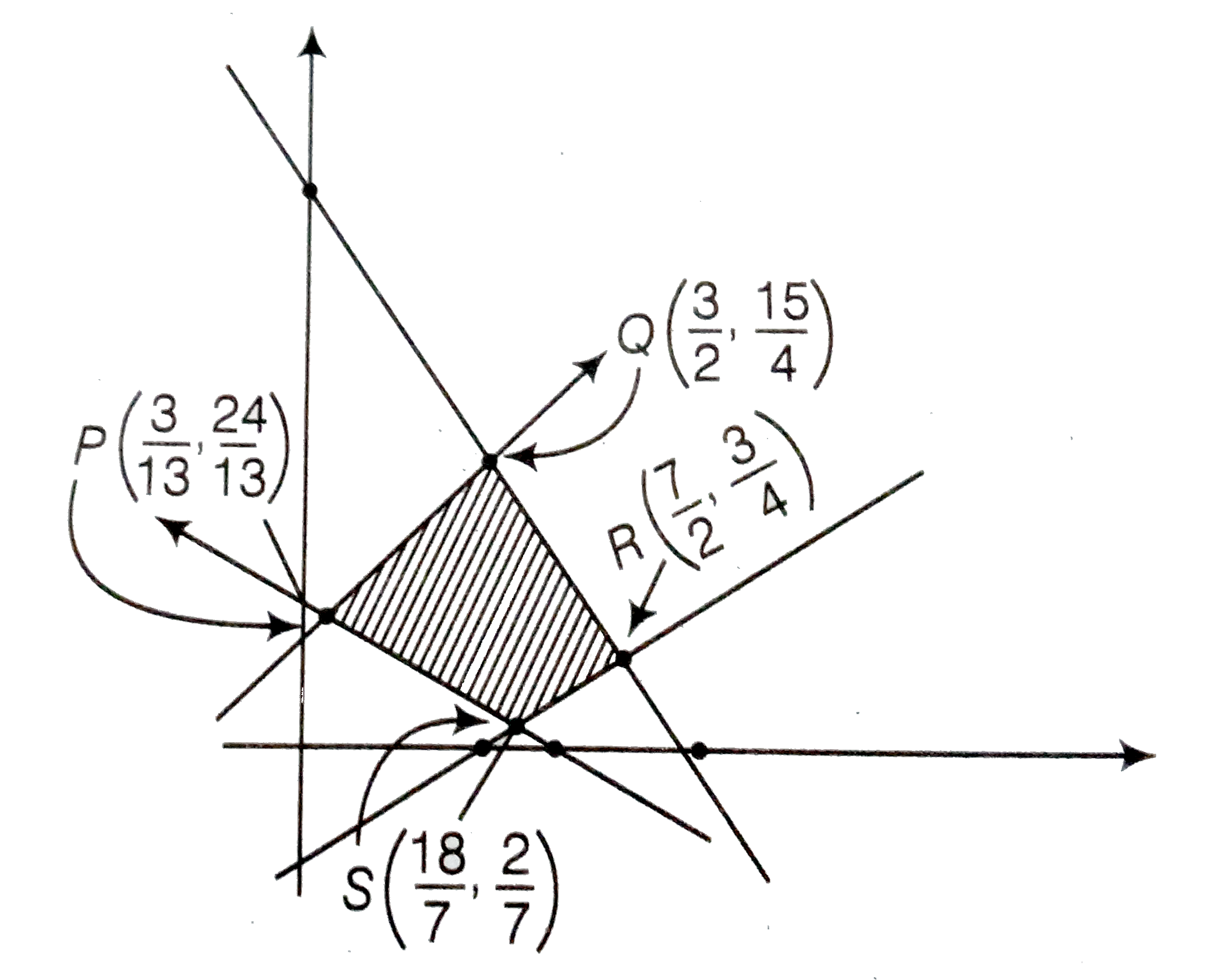
View SolutionIf the objective function for an L.P.P. is Z=3x+4y and the corner points for unbounded feasible region are (9, 0), (4, 3), (2, 5), and (0, 8), then the maximum value of Z occurs at
View Solution
