In a group of 400 people, 160 are smokers and non-vegetarian, 100 are smokers and vegetarian and the remaining are non-smokers and vegetarian. The probabilities of getting a special chest disease are 35%,,20% and 10% respectively. A person is chosen from the group at random and is found to be suffering from the disease. What is the probability that the selected person is a smoker and non-vegetarian?

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem step by step, we will use Bayes' theorem to find the probability that a randomly selected person suffering from the disease is a smoker and non-vegetarian.
Step 1: Define the Events
Let:
- $E_{1}$ : The event that a person is a smoker and non-vegetarian.
- $E_{2}$ : The event that a person is a smoker and vegetarian.
- $E_{3}$ : The event that a person is a non-smoker and vegetarian.
- $A$ : The event that a person suffers from the disease.
Step 2: Determine the Number of People in Each Category
From the problem:
- Total number of people = 400
- Number of smokers and non-vegetarians ( $E_{1}$ ) = 160
- Number of smokers and vegetarians ( $E_{2}$ ) = 100
- Number of non-smokers and vegetarians ( $E_{3}$ ) = Total - ( $E_{1} + E_{2}$ ) = $400 - (160 + 100) = 140$
Step 3: Calculate the Probabilities of Each Event
- $P (E_{1}) = \frac{160}{400} = 0.4$
- $P (E_{2}) = \frac{100}{400} = 0.25$
- $P (E_{3}) = \frac{140}{400} = 0.35$
Step 4: Determine the Probabilities of Disease Given Each Event
From the problem:
- Probability of getting the disease if a person is a smoker and non-vegetarian: $P (A | E_{1}) = 0.35$
- Probability of getting the disease if a person is a smoker and vegetarian: $P (A | E_{2}) = 0.20$
- Probability of getting the disease if a person is a non-smoker and vegetarian: $P (A | E_{3}) = 0.10$
Step 5: Apply Bayes' Theorem
We want to find $P (E_{1} | A)$ , which is the probability that a person is a smoker and non-vegetarian given that they have the disease. According to Bayes' theorem:
$P (E_{1} | A) = \frac{P (E_{1}) \cdot P (A | E_{1})}{P (E_{1}) \cdot P (A | E_{1}) + P (E_{2}) \cdot P (A | E_{2}) + P (E_{3}) \cdot P (A | E_{3})}$
Step 6: Substitute the Values
Substituting the values we calculated:
$P (E_{1} | A) = \frac{(\frac{160}{400}) \cdot (\frac{35}{100})}{(\frac{160}{400}) \cdot (\frac{35}{100}) + (\frac{100}{400}) \cdot (\frac{20}{100}) + (\frac{140}{400}) \cdot (\frac{10}{100})}$
Step 7: Calculate the Numerator and Denominator
Numerator:
$\frac{160}{400} \cdot \frac{35}{100} = \frac{5600}{40000}$
Denominator:
$\frac{160}{400} \cdot \frac{35}{100} + \frac{100}{400} \cdot \frac{20}{100} + \frac{140}{400} \cdot \frac{10}{100}$
Calculating each term:
1. $\frac{5600}{40000}$
2. $\frac{100}{400} \cdot \frac{20}{100} = \frac{2000}{40000}$
3. $\frac{140}{400} \cdot \frac{10}{100} = \frac{1400}{40000}$
Now, summing these:
$\frac{5600 + 2000 + 1400}{40000} = \frac{9000}{40000}$
Step 8: Final Calculation
Now substituting back into Bayes' theorem:
$P (E_{1} | A) = \frac{\frac{5600}{40000}}{\frac{9000}{40000}} = \frac{5600}{9000} = \frac{28}{45}$
Conclusion
The probability that the selected person is a smoker and non-vegetarian given that they are suffering from the disease is $\frac{28}{45}$ .

Updated on:7/8/2024

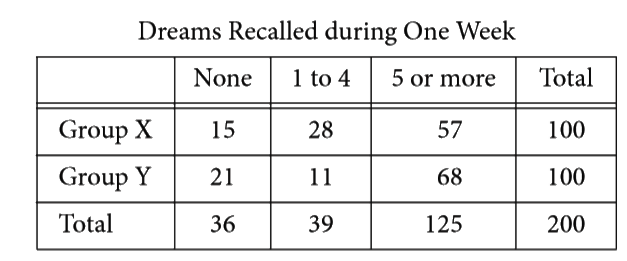
The data in the table above were produced by a sleep researcher studying the number of dreams people recall when asked to record their dreams for one week. Group X consisted of 100 people who observed early bedtimes, and Group Y consisted of 100 people who observed later bedtimes. If a person is chosen at random from those who recalled at least 1 dream, what is the probability that the person belonged to Group Y ?
A $\frac{68}{100}$
B $\frac{79}{100}$
C $\frac{79}{164}$
D $\frac{164}{200}$