Pair of fair dice is thrown. Let X be the random variable which denotes the minimum of the two numbers which appear. Find the probability distribution, mean and variance of X.
To solve the problem of finding the probability distribution, mean, and variance of the random variable X, which denotes the minimum of the two numbers appearing when a pair of fair dice is thrown, we can follow these steps:
Step 1: Identify the Sample Space
When two dice are thrown, the total number of outcomes is 6×6=36. The sample space consists of all pairs (a,b) where a and b can take values from 1 to 6.
Step 2: Define the Random Variable X
The random variable X represents the minimum of the two numbers appearing on the dice. Therefore, X can take values from 1 to 6.
Step 3: Calculate the Probability Distribution of X
We need to find the probability P(X=k) for k=1,2,3,4,5,6.
- For X=1: The pairs where the minimum is 1 are:
- (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
- (2,1), (3,1), (4,1), (5,1), (6,1)
Total outcomes = 11.
Probability P(X=1)=1136.
- For X=2: The pairs where the minimum is 2 are:
- (2,2), (2,3), (2,4), (2,5), (2,6)
- (3,2), (4,2), (5,2), (6,2)
Total outcomes = 9.
Probability P(X=2)=936=14.
- For X=3: The pairs where the minimum is 3 are:
- (3,3), (3,4), (3,5), (3,6)
- (4,3), (5,3), (6,3)
Total outcomes = 7.
Probability P(X=3)=736.
- For X=4: The pairs where the minimum is 4 are:
- (4,4), (4,5), (4,6)
- (5,4), (6,4)
Total outcomes = 5.
Probability P(X=4)=536.
- For X=5: The pairs where the minimum is 5 are:
- (5,5), (5,6)
- (6,5)
Total outcomes = 3.
Probability P(X=5)=336=112.
- For X=6: The only pair where the minimum is 6 is:
- (6,6)
Total outcomes = 1.
Probability P(X=6)=136.
Step 4: Summarize the Probability Distribution
The probability distribution of X is:
- P(X=1)=1136
- P(X=2)=936
- P(X=3)=736
- P(X=4)=536
- P(X=5)=336
- P(X=6)=136
Step 5: Calculate the Mean of X
The mean E(X) is calculated as:
E(X)=6∑i=1i⋅P(X=i)=1⋅1136+2⋅936+3⋅736+4⋅536+5⋅336+6⋅136
Calculating this gives:
E(X)=11+18+21+20+15+636=9136≈2.53
Step 6: Calculate the Variance of X
The variance Var(X) is calculated using the formula:
Var(X)=E(X2)−(E(X))2
First, we need to calculate E(X2):
E(X2)=6∑i=1i2⋅P(X=i)=12⋅1136+22⋅936+32⋅736+42⋅536+52⋅336+62⋅136
Calculating this gives:
E(X2)=11+36+63+80+75+3636=30136
Now, substituting back into the variance formula:
Var(X)=30136−(9136)2=30136−82811296
Finding a common denominator and simplifying gives:
Var(X)=301⋅36−82811296=10836−82811296=25551296≈1.97
Final Results
- Probability Distribution:
- P(X=1)=1136
- P(X=2)=936
- P(X=3)=736
- P(X=4)=536
- P(X=5)=336
- P(X=6)=136
- Mean E(X)≈2.53
- Variance Var(X)≈1.97
When two dice are thrown, the total number of outcomes is 6×6=36. The sample space consists of all pairs (a,b) where a and b can take values from 1 to 6.
The random variable X represents the minimum of the two numbers appearing on the dice. Therefore, X can take values from 1 to 6.
We need to find the probability P(X=k) for k=1,2,3,4,5,6.
- (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
- (2,1), (3,1), (4,1), (5,1), (6,1)
Total outcomes = 11.
Probability P(X=1)=1136.
- (2,2), (2,3), (2,4), (2,5), (2,6)
- (3,2), (4,2), (5,2), (6,2)
Total outcomes = 9.
Probability P(X=2)=936=14.
- (3,3), (3,4), (3,5), (3,6)
- (4,3), (5,3), (6,3)
Total outcomes = 7.
Probability P(X=3)=736.
- (4,4), (4,5), (4,6)
- (5,4), (6,4)
Total outcomes = 5.
Probability P(X=4)=536.
- (5,5), (5,6)
- (6,5)
Total outcomes = 3.
Probability P(X=5)=336=112.
- (6,6)
Total outcomes = 1.
Probability P(X=6)=136.
The probability distribution of X is:
- P(X=1)=1136
- P(X=2)=936
- P(X=3)=736
- P(X=4)=536
- P(X=5)=336
- P(X=6)=136
The mean E(X) is calculated as:
E(X)=6∑i=1i⋅P(X=i)=1⋅1136+2⋅936+3⋅736+4⋅536+5⋅336+6⋅136
Calculating this gives:
E(X)=11+18+21+20+15+636=9136≈2.53
The variance Var(X) is calculated using the formula:
Var(X)=E(X2)−(E(X))2
First, we need to calculate E(X2):
E(X2)=6∑i=1i2⋅P(X=i)=12⋅1136+22⋅936+32⋅736+42⋅536+52⋅336+62⋅136
Calculating this gives:
E(X2)=11+36+63+80+75+3636=30136
Now, substituting back into the variance formula:
Var(X)=30136−(9136)2=30136−82811296
Finding a common denominator and simplifying gives:
Var(X)=301⋅36−82811296=10836−82811296=25551296≈1.97
- Probability Distribution:
- P(X=1)=1136
- P(X=2)=936
- P(X=3)=736
- P(X=4)=536
- P(X=5)=336
- P(X=6)=136
- Variance Var(X)≈1.97
Topper's Solved these Questions
Similar Questions
A coin weighted so that P(H)=34andP(T)=14 is tossed three times. Let X be the random variable which denotes the longer string of heads which occurs. Find the probability distribution, mean and variance of X.
View SolutionA pair of fair dice is rolled at a time. The random variable X is the maximum of the two numbers shows on the dice. Find the probability distribution of X and mean of X.
View SolutionA fair die is tossed. Let X denote twice the number appearing. Find the probability distribution, mean and variance of X.
View SolutionConsider the probability distribution of a random variable X.

Variance of X
View SolutionA fair coin is tossed four times. Let X denote the number of heads occurring. Find the probability distribution, mean and variance of X.
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View SolutionA fair die is tossed. Let X denote 1 or 3 according as an odd or an even number appears. Find the probability distribution, means variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionIf X is a random variable with the following probability distribution
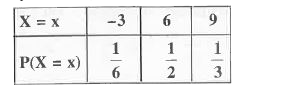
then the variance of X is
View Solution
