If the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
To find the value of k in the given probability distribution of the random variable X, we need to ensure that the sum of all probabilities equals 1.
The random variable X takes the values xi=1,2,3,4 with corresponding probabilities P(X=xi)=2k,4k,3k,k.
1. Write down the probabilities:
P(X=1)=2k,P(X=2)=4k,P(X=3)=3k,P(X=4)=k
2. Set up the equation for the total probability:
The sum of all probabilities must equal 1:
2k+4k+3k+k=1
3. Combine like terms:
Combine the coefficients of k:
(2+4+3+1)k=1
Simplifying gives:
10k=1
4. Solve for k:
Divide both sides by 10:
k=110
5. Conclusion:
The value of k is:
k=110
P(X=1)=2k,P(X=2)=4k,P(X=3)=3k,P(X=4)=k
The sum of all probabilities must equal 1:
2k+4k+3k+k=1
Combine the coefficients of k:
(2+4+3+1)k=1
Simplifying gives:
10k=1
Divide both sides by 10:
k=110
The value of k is:
k=110
Topper's Solved these Questions
Similar Questions
If the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
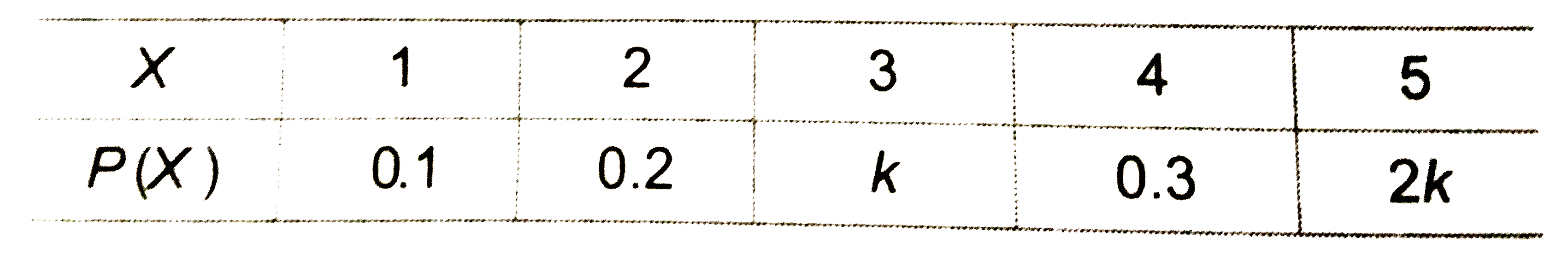
View Solution
