Two brands of chocolates are available in packs of 24 and 15 respectively. If I need to buy an equal number of chocolates of both kinds, what is the least number of boxes of each kind I would need to buy?
To solve the problem of how many boxes of each kind of chocolate you need to buy to have an equal number of chocolates, we will find the least common multiple (LCM) of the two pack sizes: 24 and 15.
1. Identify the Pack Sizes:
- Brand 1 has packs of 24 chocolates.
- Brand 2 has packs of 15 chocolates.
2. Find the LCM of 24 and 15:
- To find the LCM, we can use the prime factorization method.
- Prime Factorization:
- 24 = 2 × 2 × 2 × 3 = 23×31
- 15 = 3 × 5 = 31×51
3. Determine the LCM:
- The LCM is found by taking the highest power of each prime factor from both numbers.
- From 24: 23 and 31
- From 15: 31 and 51
- Therefore, the LCM is:
LCM=23×31×51=8×3×5
- Calculate:
8×3=24
24×5=120
- So, the LCM of 24 and 15 is 120.
4. Calculate the Number of Boxes Needed:
- To find out how many boxes of each brand are needed to reach 120 chocolates:
- For Brand 1 (24 chocolates per box):
Number of boxes=12024=5
- For Brand 2 (15 chocolates per box):
Number of boxes=12015=8
5. Final Answer:
- You need to buy 5 boxes of Brand 1 and 8 boxes of Brand 2 to have an equal number of chocolates.
- Brand 1 has packs of 24 chocolates.
- Brand 2 has packs of 15 chocolates.
- To find the LCM, we can use the prime factorization method.
- Prime Factorization:
- 24 = 2 × 2 × 2 × 3 = 23×31
- 15 = 3 × 5 = 31×51
- The LCM is found by taking the highest power of each prime factor from both numbers.
- From 24: 23 and 31
- From 15: 31 and 51
- Therefore, the LCM is:
LCM=23×31×51=8×3×5
- Calculate:
8×3=24
24×5=120
- So, the LCM of 24 and 15 is 120.
- To find out how many boxes of each brand are needed to reach 120 chocolates:
- For Brand 1 (24 chocolates per box):
Number of boxes=12024=5
- For Brand 2 (15 chocolates per box):
Number of boxes=12015=8
- You need to buy 5 boxes of Brand 1 and 8 boxes of Brand 2 to have an equal number of chocolates.
Topper's Solved these Questions
Similar Questions
Three brands B1, B2 and B3 of shirts are available in cartons of 12, 15 and 21 shirts respectively. A stockist wants to stock the same number of shirts of each brand in his warehouse. What is the minimum number of cartons of each brand that he nneds to buy?
View SolutionDuring a sale, colour pencils were being sold in packs of 24 each and crayons in packs of 32 each. If you want full packs of both and the same number of pencils and crayons, how many of each would you need to buy?
View Solution
Knowledge Check
- Question 1 - Select One
Preeti baked 352 butter cream cookies, 448 cashew nut cookies and 736 choconut cookies to sell at her stall in a fair. She wants to pack the cookies in packets so that each packet has the same number of cookies of the same kind. If she wants to pack the largest number of cookies possible in each packet, how many packets will she need to pack ? Also find the number of packets of each kind of cookies
ATotal number of packets −48
Butter cream cookies −11
Cashew nut cookies −14
Choconut cookies −23BTotal number of packets −48
Butter cream cookies −11
Cashew nut cookies −23
Choconut cookies −14CTotal number of packets −38
Butter cream cookies −9
Cashew nut cookies −6
Choconut cookies −23DTotal number of packets −38
Butter cream cookies −11
Cashew nut cookies −14
Choconut cookies −13 - Question 2 - Select One
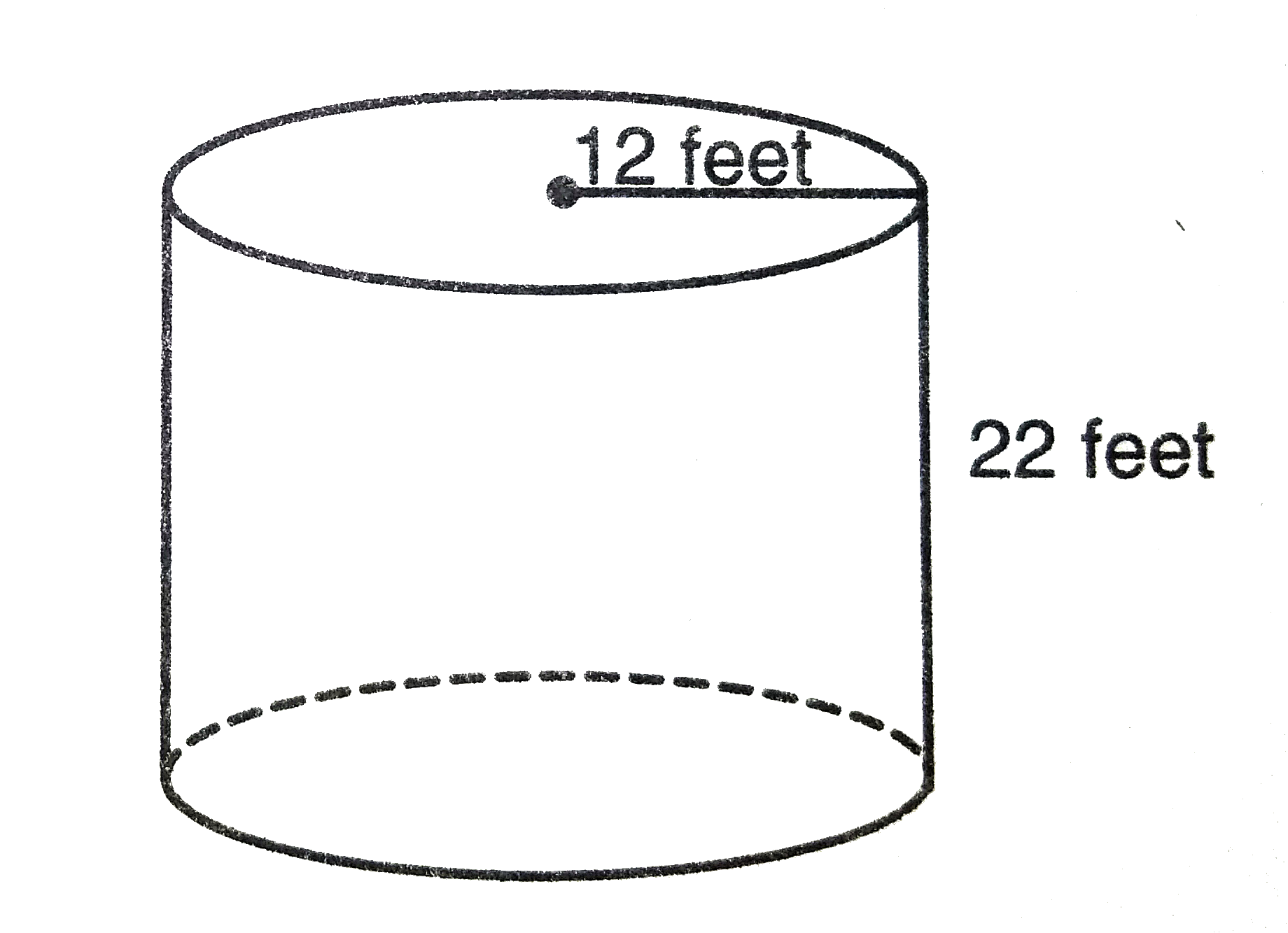
The cylinderical tank shown in the diagram above is to be painted. The tank is open at the top, and the bottom does not need to be painted. Only the outside needs to be painted. Each can of paint covers 500 square feet. What is the least number of cans of paint that must be purchased to complete the job?A2B3C4D5 - Question 3 - Select One
The most popular items at a bakery are its raspberry scones and its lemon poppy seed muffins. The shop sells both items in boxes of 12 at a cost of $15 per box of raspberry scones and $9 per box of lemon poppy seed muffins. On Friday and Saturday, the shop earned $396 by selliing a total of 46 boxes of these two items. If r and l represent the number of boxes of raspberry scones and lemon poppy seed muffins sold over the two-day period, respectively, which of the following systems of equations could be used to find the number of boxes of each type of item sold?
Ar+l=46
15r+9l=396Br+l=12×46
15r+9l=396Cr+l=46
15r+9l=3962Dr+l=12×46
15r+9l=39612
During a sale, colour pencils were being sold in packs of 24 each and crayons in packs of 32 each. If you want full packs of both and the same number of pencils and crayons, how many of each would you need to buy?
View SolutionParul has 5 boxes of chocolates containing 90 chocolates each. If she kept 10 chocolates for herself, would it be possible for her to empty them into 11 packets with equal number of chocolates in each packet? Also, give the number of chocolates in each packet.
View SolutionThere are two confectioneries in a locality. The number of chocolate boxes in the first shop is 250 less than twice the number of chocolate boxes available in the second shop. By the end of the day, the first shop has sold 350 boxes and the second shop has sold 200 boxes. The number of boxes left unsold in both the shops is equal. Find the number of chocolates in both the shops at the beginning of the day.
View SolutionThere are two bags each of which contains n balls. A man has to select an equal number of balls from both the bags. Prove that the number of ways in which a man can choose at least one ball from each bag is2nCn−1.
View SolutionThere are two bags each of which contains n balls. A man has to select an equal number of balls from both the bags. Prove that the number of ways in which a man can choose at least one ball from each bag is2nCn−1.
View Solution

