Four bells toll at intervals of 4, 7, 12 and 84 seconds. The bells toll together at 5 O’clock. When will they again toll together? How many times will they do it in 28 minutes?
To solve the problem step by step, we will find the least common multiple (LCM) of the intervals at which the bells toll, and then determine how many times they toll together in 28 minutes.
Step 1: Identify the intervals
The intervals at which the bells toll are:
- Bell 1: 4 seconds
- Bell 2: 7 seconds
- Bell 3: 12 seconds
- Bell 4: 84 seconds
Step 2: Find the LCM of the intervals
To find when all four bells will toll together again, we need to calculate the LCM of the numbers 4, 7, 12, and 84.
1. Prime factorization of each number:
- 4 = 2²
- 7 = 7¹
- 12 = 2² × 3¹
- 84 = 2² × 3¹ × 7¹
2. Identify the highest power of each prime factor:
- For 2: highest power is 2² (from 4, 12, and 84)
- For 3: highest power is 3¹ (from 12 and 84)
- For 7: highest power is 7¹ (from 7 and 84)
3. Calculate the LCM:
\text{LCM} = 2² × 3¹ × 7¹ = 4 × 3 × 7
=12×7=84
Step 3: Determine the time when they toll together again
The bells toll together again after 84 seconds. Since they toll together at 5:00 PM, we add 84 seconds to this time.
- 84 seconds = 1 minute and 24 seconds.
- Therefore, they will toll together again at:
5:00:00+00:01:24=5:01:24 PM
Step 4: Calculate how many times they toll together in 28 minutes
Next, we need to find out how many times they toll together in 28 minutes.
1. Convert 28 minutes to seconds:
28 minutes=28×60=1680 seconds
2. Calculate the number of times they toll together:
We divide the total seconds by the interval at which they toll together:
Number of times=1680 seconds84 seconds=20
Final Answer
The bells will toll together again at 5:01:24 PM, and they will toll together 20 times in 28 minutes.
---
The intervals at which the bells toll are:
- Bell 1: 4 seconds
- Bell 2: 7 seconds
- Bell 3: 12 seconds
- Bell 4: 84 seconds
To find when all four bells will toll together again, we need to calculate the LCM of the numbers 4, 7, 12, and 84.
- 4 = 2²
- 7 = 7¹
- 12 = 2² × 3¹
- 84 = 2² × 3¹ × 7¹
- For 2: highest power is 2² (from 4, 12, and 84)
- For 3: highest power is 3¹ (from 12 and 84)
- For 7: highest power is 7¹ (from 7 and 84)
\text{LCM} = 2² × 3¹ × 7¹ = 4 × 3 × 7
=12×7=84
The bells toll together again after 84 seconds. Since they toll together at 5:00 PM, we add 84 seconds to this time.
- Therefore, they will toll together again at:
5:00:00+00:01:24=5:01:24 PM
Next, we need to find out how many times they toll together in 28 minutes.
28 minutes=28×60=1680 seconds
We divide the total seconds by the interval at which they toll together:
Number of times=1680 seconds84 seconds=20
The bells will toll together again at 5:01:24 PM, and they will toll together 20 times in 28 minutes.
Topper's Solved these Questions
Similar Questions
Three bells ring at an interval of 4, 7 and 12 seconds. They start to ring together at 7.00 a.m. When will they ring together again ?
View SolutionThree bells ring at intervals of 4,7and14 minutes. All three range at 6 am. When will they ring together again ?
View SolutionThree bells toll every 6 minutes, 8 minutes and 12 minutes respectively. If they all start tolling at 8.00 a.m. at what time will they toll together again?
View SolutionThree bells are ringing continuously at intervals of 30, 36 and 45 minutes respectively. At what time will they ring together again if they ring simultaneously at 8 a.m. ?
View SolutionFive bells begins to toll together and toll respectively at intervals 6,7,8,9 and 12 seconds. How many times will they toll together in one hour, excluding the one at the start?
View SolutionSix bells commence tolling together and toll at interval of 2, 4 , 6, 8 , 10 , 12 minutes respectively . In 30 hours , how many times do they toll together ?
View Solution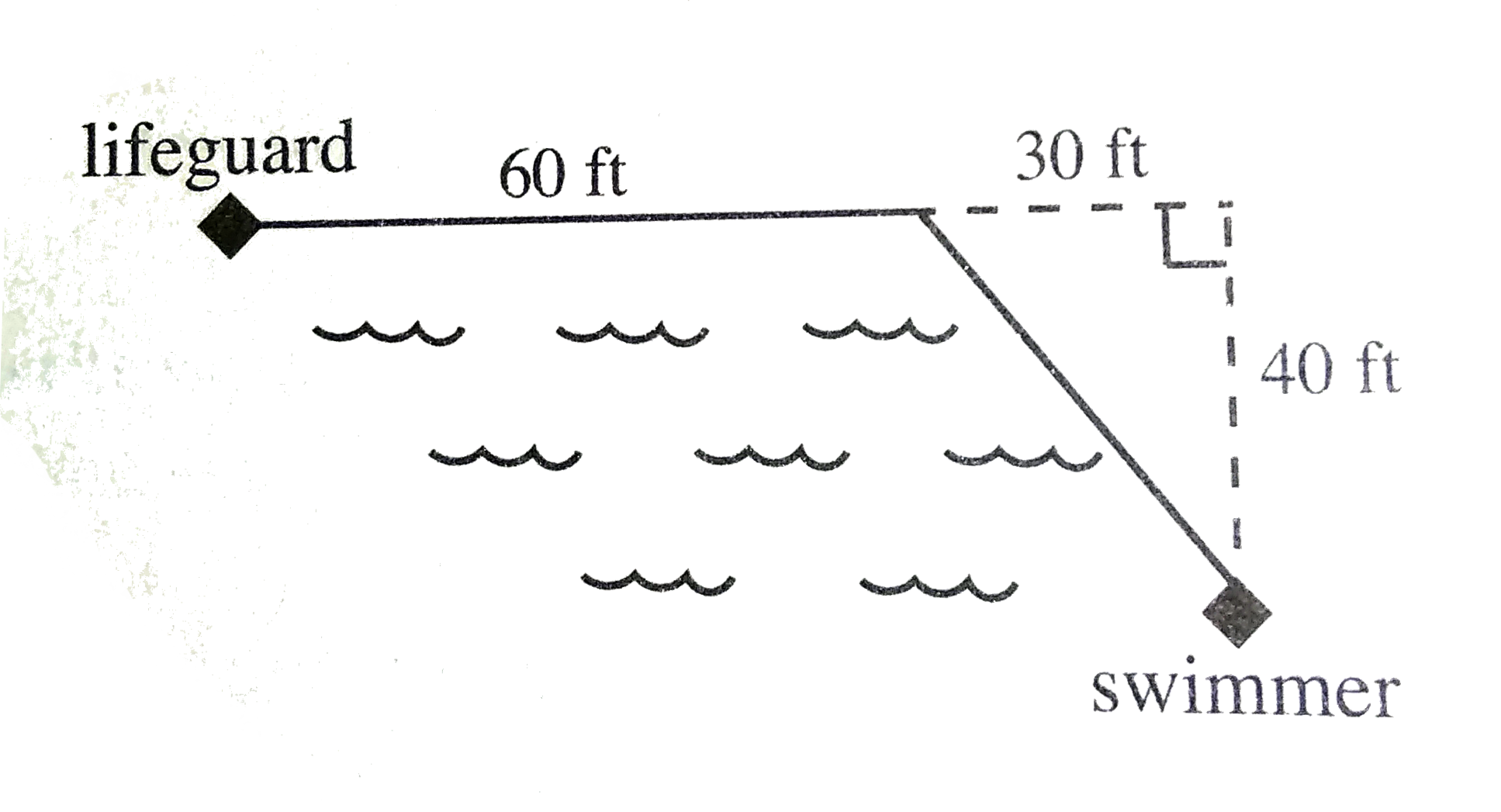
As shown in the figure above, a lifeguard sees a struggling swimmer who is 40 feet from the beach. The lifeguard runs 60 feets along the edge of the water at a speed of 12 feet per second. He pauses for 1 seconds to locate the swimmer again, and then dives into the water and swims along a diagonal path to the swimmer at a speed of 5 feet per second. How many seconds go by between the time the lifeguard sees the struggling swimmer and the times he reaches the swimmer?
View SolutionIn a school, the bell for the middle school rings every 30 minutes and the bell for the senior school rings every 40 minutes. The two bells start to ring together at 8.00 a.m. At what time will they ring together again?
View SolutionA delegation of four students is to be selected from al total of 12 students. In how many says can the delegation be selected. if all the students are equally willing? if two particular students have to be included in the delegation? if two particular students do not wish to be together in the delegation? if two particular students wish to be included together only in the delegation? if two particular students refuse to be together and two other particular students wish to be together only in the delegation?
View SolutionThe time represented by the clock hands of a pendulum clock depends on the number of oscillations performed by pendulum. Every time it reaches to its exterme position the second hand of the clock advances by one second that means second hand moves by two second when one oscillation is completed.
(a) How many number of oscillations completed by pendulum of clock in 15 minutes at calibrated temperature 20∘C
(b) How many number of oscillations are completed by a pendulum of clock in 15 minutes at temperature of 40∘Cifα=2×10−5/∘C
(c ) What time is represented by the pendulum clock at 40∘C after 15 minutes if the initial time shown by the clock is 12:00 pm?
(d) If the clock gains two seconds in 15 minutes in correct clock then find-(i) Number of extra oscillations (ii) New time period (iii) change in temperature.
View Solution
