In a school there are two sections - section A and section B of Class VI. There are 32 students in section A and 36 in section B. Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B.
To solve the problem of finding the minimum number of books required for the class library that can be distributed equally among the students of section A (32 students) and section B (36 students), we need to determine the Least Common Multiple (LCM) of the two numbers.
1. Identify the number of students in each section:
- Section A has 32 students.
- Section B has 36 students.
2. Understand the requirement:
- We need to find a number of books that can be evenly distributed among both sections. This means the number of books must be a multiple of both 32 and 36.
3. Find the prime factorization of each number:
- For 32:
- 32=25
- For 36:
- 36=22×32
4. Determine the LCM using the highest powers of all prime factors:
- The prime factors involved are 2 and 3.
- For 2, the highest power is 25 (from 32).
- For 3, the highest power is 32 (from 36).
- Therefore, the LCM is calculated as:
LCM=25×32
5. Calculate the LCM:
- First, calculate 25=32.
- Next, calculate 32=9.
- Now, multiply these results:
LCM=32×9=288
6. Conclusion:
- The minimum number of books required for the class library is 288.
- Section A has 32 students.
- Section B has 36 students.
- We need to find a number of books that can be evenly distributed among both sections. This means the number of books must be a multiple of both 32 and 36.
- For 32:
- 32=25
- For 36:
- 36=22×32
- The prime factors involved are 2 and 3.
- For 2, the highest power is 25 (from 32).
- For 3, the highest power is 32 (from 36).
- Therefore, the LCM is calculated as:
LCM=25×32
- First, calculate 25=32.
- Next, calculate 32=9.
- Now, multiply these results:
LCM=32×9=288
- The minimum number of books required for the class library is 288.
Topper's Solved these Questions
Similar Questions
In a school there are two sections section A and section B of class X . There are 32 students in section A and 36 students in section B . Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B .
View SolutionIn a school there are five sections of class IX. The number of students in each section is given below.
Construct a bar graph.

View SolutionThere are 100 students in class VII in a school. 40 students are in Section A, 33 in Section B, and the remaining students are in Section C. Find what percentage of students are there in each section.
View SolutionThe number of students in section X A and X B are 30 and 35 respectively. The mean scores of students in the mathematices test are as follows:

View SolutionThe potential difference between points A and B, in a section of a circuit shown in
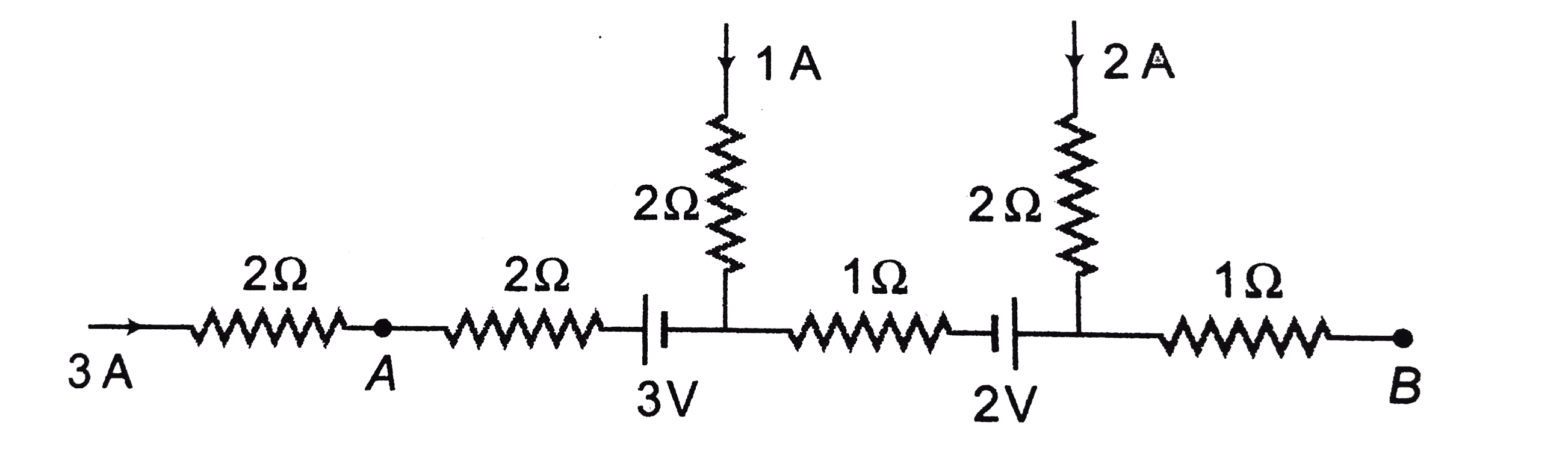
View SolutionIn a school, there are five sections of class IX. The number of students in each section is given below. Construct a bar graph representing this data: Section: A B C D E No. of Students 40 48 52 45 30
View SolutionIn a school, there are five sections of class VII. The number of students in each section is given below. Construct a bar graph representing this data: Section, A, B, C, D, E No. of Students, 40, 48, 52, 45, 30
View SolutionIn a cross section of the spinal cord A, B, C, D and E represent

View SolutionThere are three sections in a question paper, each containing 5 questions. A candidate has to solve any 5 questions, choosing at least one from each section. Find the number of ways in which the candidate can choose the questions.
View SolutionThe figure shows a section of human ovary . Select the option which gives the correct identification of A and B with function // characteristic

View Solution
