In Figure, name the (i) face parallel to BFGC (ii) faces adjacent to BFGC (iii) three edges which meet in the vertex G.
To solve the question step by step, let's break it down into three parts as asked:
Step 1: Identify the face parallel to BFGC
1. Identify the face BFGC: In a cuboid, the face BFGC is defined by the vertices B, F, G, and C.
2. Find the parallel face: The face that is parallel to BFGC will be the one that does not intersect with it and is on the opposite side of the cuboid. In this case, the face A E H D is parallel to B F G C.
Answer: The face parallel to BFGC is A E H D.
Step 2: Identify the faces adjacent to BFGC
1. Identify adjacent faces: Adjacent faces share a common edge with the face BFGC.
2. List the adjacent faces: The faces adjacent to BFGC are:
- A E B F (the face on the side)
- G H C F (the face on the front)
- G H B F (the face on the back)
Answer: The faces adjacent to BFGC are A E B F and G H C F.
Step 3: Identify the three edges that meet at vertex G
1. Locate vertex G: In the cuboid, vertex G is one of the corners.
2. Identify edges meeting at G: The edges that meet at vertex G are:
- G H (vertical edge going up)
- G C (horizontal edge going to the right)
- G F (horizontal edge going to the left)
Answer: The three edges that meet at vertex G are G H, G C, and G F.
---
1. Identify the face BFGC: In a cuboid, the face BFGC is defined by the vertices B, F, G, and C.
2. Find the parallel face: The face that is parallel to BFGC will be the one that does not intersect with it and is on the opposite side of the cuboid. In this case, the face A E H D is parallel to B F G C.
1. Identify adjacent faces: Adjacent faces share a common edge with the face BFGC.
2. List the adjacent faces: The faces adjacent to BFGC are:
- A E B F (the face on the side)
- G H C F (the face on the front)
- G H B F (the face on the back)
1. Locate vertex G: In the cuboid, vertex G is one of the corners.
2. Identify edges meeting at G: The edges that meet at vertex G are:
- G H (vertical edge going up)
- G C (horizontal edge going to the right)
- G F (horizontal edge going to the left)
Topper's Solved these Questions
Similar Questions
In Figure, If the face EFGH is taken as the base, then name the lateral faces. Also, name the line segment representing the height of the cuboid.
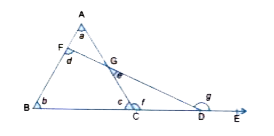
View SolutionUse the given figure to express :
(i) a in terms of b and f,
(ii) e in terms of f and g,
(iii) d in terms of a and e,
(iv) c in terms of e and g.
View SolutionThe adjoining figure represents a cuboid.
(i) How many edges does the cuboid have?
(ii) Name two edges of the cuboid which are parallel to AD .
(iii) Name two edges of the cuboid which are perpendicular to AD.

View SolutionTake three non-collinear point A, B and C on a page of your notebook. Join AB, BC and CA, what figure do you get? Name the triangle. Also, name The side opposite to ∠B The angle opposite to side AB The vertex opposite to side BC The side opposite to vertex B.
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: (i) ar(△ACB)=ar(△ACF) (ii) ar(quadrilateralAEDF)=ar(ABCDE)
View SolutionFill in the blanks to make the following statements true:
(i) A cuboid has .......... vertices.
(ii) A cuboid has .......... edges
(iii) A cuboid has .......... faces.
(iv) The number of lateral faces of a cuboid is .........
(v) A cuboid all of whose edges are equal is called a .........
(vi) Two adjacent faces of a cuboid meet in a line segment called its .........
(vii) Each edge of a cuboid can be obtained as a line segment in which two ......... meet.
(viii) ......... edges of a cube (or cuboid) meet at each of its vertices.
(ix) A ......... is a cuboid in which all the six faces are squares.
(x) The three concurrent edges of a cuboid meet at a point called the ......... of the cuboid.
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(∣∣gmEFGH)=12ar(∣∣gmABCD) CONSTRUCTION : Join AC and HF
View SolutionThe dimensions of a cuboid with vertices A, B, C, D, E, F, G and H are as shown in Figure. Which edges are of length 4cm? Which edges are of length 5cm? Which faces have area equal to 20 cm2? Which faces have the largest area? What is this largest area?
View SolutionE,F,G,H are respectively, the mid-points of the sides of parallelogram ABCD . Show that the area of EFGH is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join H and F
View SolutionConsider a cube ABCGHIJK of sides a placed in a uniform magnetic field B acting perpendicular to the face BHIC as shown in figure.
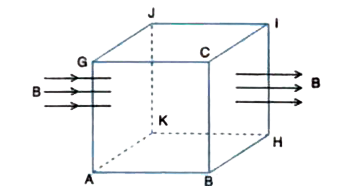
(i) What is the flux through face ABCG?
(ii) What is the flux through face GCIJ?
(iii) What is the flux through face AKJG?
(iv) What is the flux through face BHIC?
View Solution
