Question

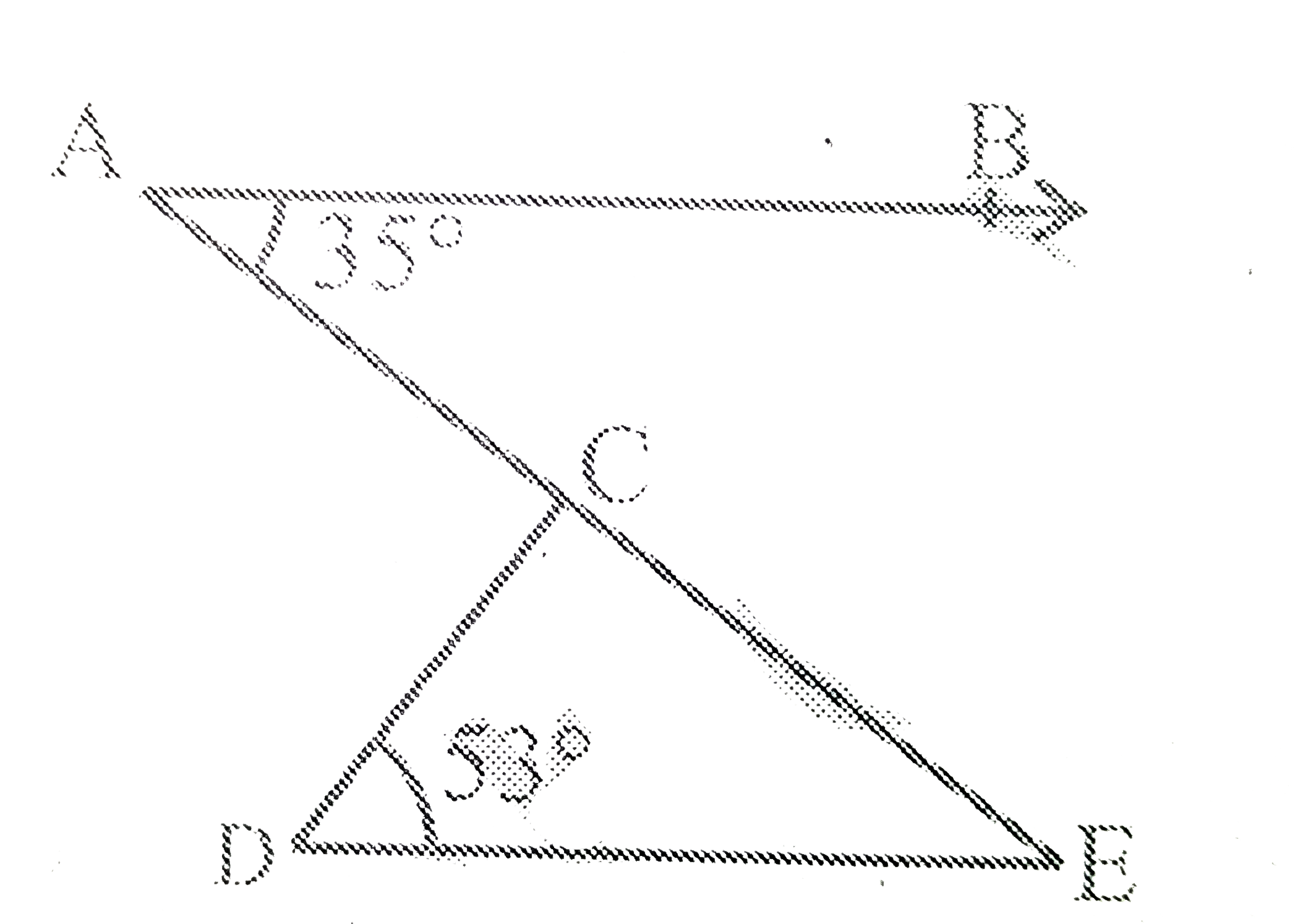
In Fig.74, if $ABCD,\angle CAB={49}^0,$
$\angle CBD={27}^{0}and\angle BCD={112}^0,$
then the values of $xandy$
are
$x=41,y=90,$
(b) $x=41,y=63,$

$x=63,y=41,$
(d) $x=90,y=41,$

Explanation

To solve the problem step by step, we will use the properties of parallel lines and triangles.

Step 1: Identify the angles
We are given:
- \( \angle CAB = 49^\circ \)
- \( \angle CBD = 27^\circ \)
- \( \angle BDC = 112^\circ \)

We need to find the values of \( x \) (which is \( \angle ABC \)) and \( y \) (which is \( \angle ACB \)).

Step 2: Use the property of parallel lines
Since \( AB \) is parallel to \( CD \) and \( BD \) is a transversal, we can use the property that states the sum of the interior angles on the same side of the transversal is \( 180^\circ \).

Thus, we have:
\( \angle ABD + \angle BDC = 180^\circ \)

Step 3: Express \( \angle ABD \)
We know that:
\( \angle ABD = x + 27^\circ \)
So we can write the equation:
\( (x + 27^\circ) + 112^\circ = 180^\circ \)

Step 4: Solve for \( x \)
Now, simplify the equation:
\( x + 139^\circ = 180^\circ \)
Subtract \( 139^\circ \) from both sides:
\( x = 180^\circ - 139^\circ \)
\( x = 41^\circ \)

Step 5: Use the angle sum property of triangle ABC
Now, we will apply the angle sum property of triangle ABC, which states that the sum of the angles in a triangle is \( 180^\circ \):
\( x + \angle CAB + y = 180^\circ \)
Substituting the known values:
\( 41^\circ + 49^\circ + y = 180^\circ \)

Step 6: Solve for \( y \)
Combine the known angles:
\( 90^\circ + y = 180^\circ \)
Subtract \( 90^\circ \) from both sides:
\( y = 180^\circ - 90^\circ \)
\( y = 90^\circ \)

Final Values
Thus, we have:
- \( x = 41^\circ \)
- \( y = 90^\circ \)

Conclusion
The values of \( x \) and \( y \) are:
- \( x = 41^\circ \)
- \( y = 90^\circ \)