If x and y vary inversely as each other, and x=10 when y=6. Find y when x=15
To solve the problem step by step, we will use the concept of inverse variation.
Step 1: Understand the relationship
Since x and y vary inversely, it means that their product is constant. This can be expressed as:
x⋅y=k
where k is a constant.
Step 2: Find the constant k
We are given that x=10 when y=6. We can use these values to find k:
k=10⋅6=60
Step 3: Set up the equation for the new values
Now we need to find y when x=15. We can use the constant k we found:
15⋅y=60
Step 4: Solve for y
To find y, we can rearrange the equation:
y=6015
Step 5: Calculate the value of y
Now, we perform the division:
y=4
Final Answer
Thus, when x=15, the value of y is:
y=4
---
Since x and y vary inversely, it means that their product is constant. This can be expressed as:
x⋅y=k
where k is a constant.
We are given that x=10 when y=6. We can use these values to find k:
k=10⋅6=60
Now we need to find y when x=15. We can use the constant k we found:
15⋅y=60
To find y, we can rearrange the equation:
y=6015
Now, we perform the division:
y=4
Thus, when x=15, the value of y is:
y=4
Topper's Solved these Questions
Similar Questions
If x and y vary inversely as each other and (i)x=3 when y=8, find y when x=4 (ii)x=5 when y=15, find x when y=12 (iii)x=3, find y when constant of variation=900. (iv)y=35, find x when constant of variation =7.
View SolutionIf x and y vary inversely, find the values of l, m and n :
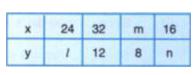
View SolutionIf x and y vary inversely, find the values of l, m and n :

View SolutionIf p and q vary inversely, find the values of x,y and z.

View SolutionIf p and q vary inversely, find the values of x,y and z.

View SolutionCheck whether x and y vary inversely or not.

View SolutionCheck whether x and y vary inversely or not.

View SolutionCheck whether x and y vary inversely or not.

View SolutionIf y=f(x)andx=g(y) are inverse functions of each other, then
View SolutionIf x and y vary directly, find the values of x, y and z :

View Solution
