It is known that for a given mass of gas, the volume v varies inversely as the pressure p . Fill in the missing entries in the following table: v (∈ cm3) ... 48 60 ... 100 ... 200 p (∈ atmospheres) 2 ... 3/2 1 ... ...
To solve the problem, we will use the concept of inverse variation, which states that if v varies inversely as p, then the product v×p=k, where k is a constant.
1. Identify the Constant k:
We know that when v=60 and p=32:
k=v×p=60×32=90
2. Fill in the Missing Values:
Now that we have k=90, we can find the missing values in the table.
- Case 1: p=2
v=kp=902=45
- Case 2: v=48
p=kv=9048=158
- Case 3: p=1
v=kp=901=90
- Case 4: v=100
p=kv=90100=910
- Case 5: p=12
v=kp=9012=90×2=180
- Case 6: v=200
p=kv=90200=920
3. Final Table:
Now we can compile all the values into the final table:
| v (in cm³) | 48 | 60 | 90 | 100 | 180 | 200 |
|------------------|-----|-----|-----|-----|-----|-----|
| p (in atm) | 15/8| 3/2 | 1 | 9/10| 1/2 | 9/20|
We know that when v=60 and p=32:
k=v×p=60×32=90
Now that we have k=90, we can find the missing values in the table.
v=kp=902=45
p=kv=9048=158
v=kp=901=90
p=kv=90100=910
v=kp=9012=90×2=180
p=kv=90200=920
Now we can compile all the values into the final table:
|------------------|-----|-----|-----|-----|-----|-----|
| p (in atm) | 15/8| 3/2 | 1 | 9/10| 1/2 | 9/20|
Topper's Solved these Questions
Similar Questions
A given sample of an ideal gas occupise a volume V at a pressure p and absolute temperature T.The mass of each molecule of the gas is m. Which of the following is the density of the gas ?
View SolutionA plot of P vs T for a given mass of gas at constant volume is a straight line . P vs T at constant volumes V1 and V2 for an ideal gas are shown below :
Which of the following is correct ?
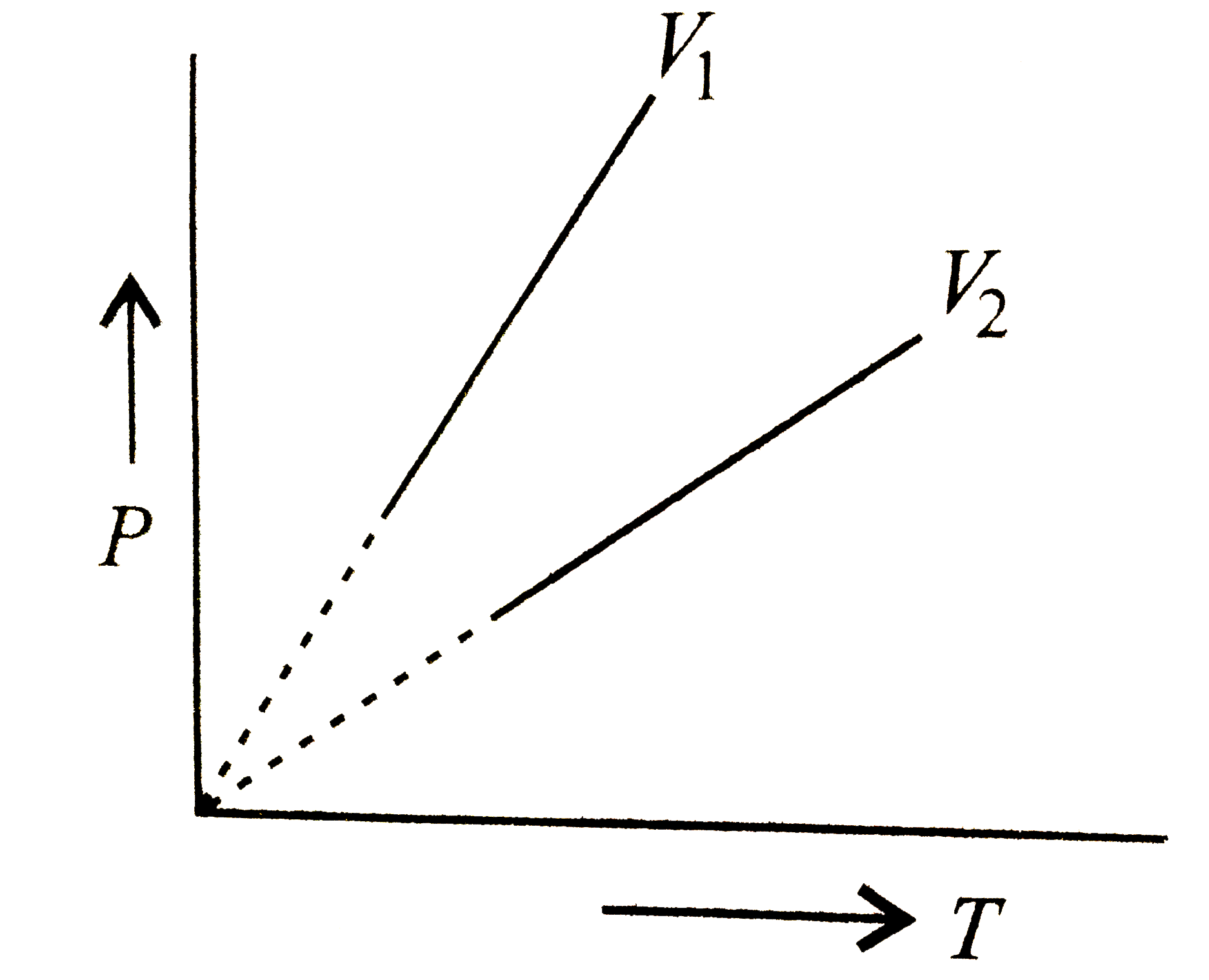
View SolutionFor V versus T curves at constant pressure P1andP2 for an ideal gas are shown in the figure given below
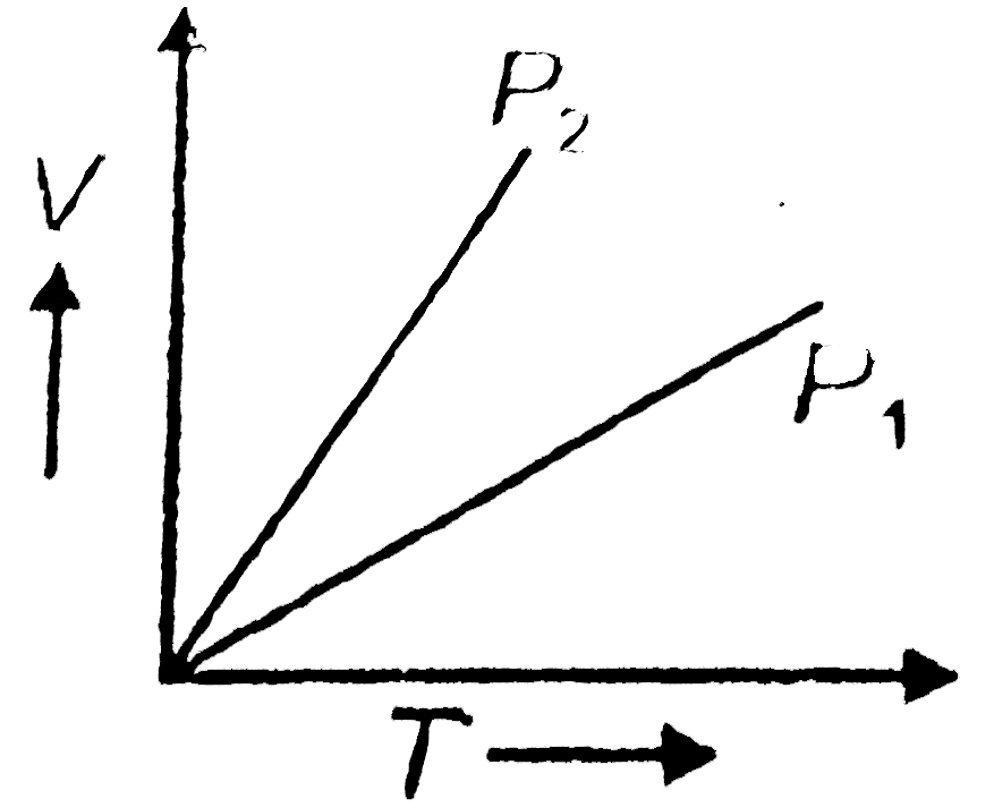
View SolutionFor an ideal gas V−T curves at constant pressure P1 & P2 are shown in figure, from the figure
_E01_061_Q01.png)
View SolutionAt constant temperature, the effect of change of pressure on volume of a gas was as given below

Plot the following graphs :
P vs 1/V
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View SolutionFigure shows volume - temperature (V-T) graph for same mass of an ideal gas at two different pressures P1and P2. Hence
View SolutionAssertion Pressure of a gas id given as p=23E.
Reason In the above expession, E represnts kinetic energy of the gas per unit volume.
View SolutionA monoatomic gas at a pressure p, having a volume 2V and then adiabatically to a volume 16 V. The final pressure of the gas is (take γ=53 )
View SolutionThe pressure p and the volume v of a gas are connected by the relation pv1.4=const. Find the percentage error in p corresponding to a decrease of 1/2 % in v.
View Solution
