In Figure, find the measure of ∠MPN
To find the measure of angle ∠MPN in the given quadrilateral NPMO, we will follow these steps:
1. Understand the Properties of Quadrilaterals:
- The sum of all interior angles in a quadrilateral is 360∘.
2. Identify Given Angles:
- From the figure, we know:
- ∠NPO=90∘ (right angle)
- ∠PMO=90∘ (right angle)
- ∠NOM=45∘
3. Set Up the Equation:
- According to the properties of quadrilaterals, we can write the equation for the sum of angles:
∠NPO+∠MPN+∠PMO+∠NOM=360∘
- Substituting the known values:
90∘+∠MPN+90∘+45∘=360∘
4. Simplify the Equation:
- Combine the known angles:
90∘+90∘+45∘=225∘
- So the equation becomes:
225∘+∠MPN=360∘
5. Solve for ∠MPN:
- Rearranging the equation gives:
∠MPN=360∘−225∘
- Calculating the right side:
∠MPN=135∘
Final Answer:
Thus, the measure of ∠MPN is 135∘.
---
- The sum of all interior angles in a quadrilateral is 360∘.
- From the figure, we know:
- ∠NPO=90∘ (right angle)
- ∠PMO=90∘ (right angle)
- ∠NOM=45∘
- According to the properties of quadrilaterals, we can write the equation for the sum of angles:
∠NPO+∠MPN+∠PMO+∠NOM=360∘
- Substituting the known values:
90∘+∠MPN+90∘+45∘=360∘
- Combine the known angles:
90∘+90∘+45∘=225∘
- So the equation becomes:
225∘+∠MPN=360∘
- Rearranging the equation gives:
∠MPN=360∘−225∘
- Calculating the right side:
∠MPN=135∘
Thus, the measure of ∠MPN is 135∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure below, line m is perpendicular to line n, and both lines intersect line q at the same point. The measure of ∠1 is (3x−10)∘, and the measure of ∠2 is (2x+10)∘. What is the measure of ∠3?
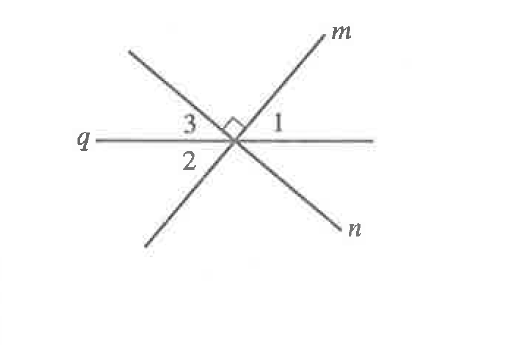 A36∘B40∘C44∘D45∘
A36∘B40∘C44∘D45∘
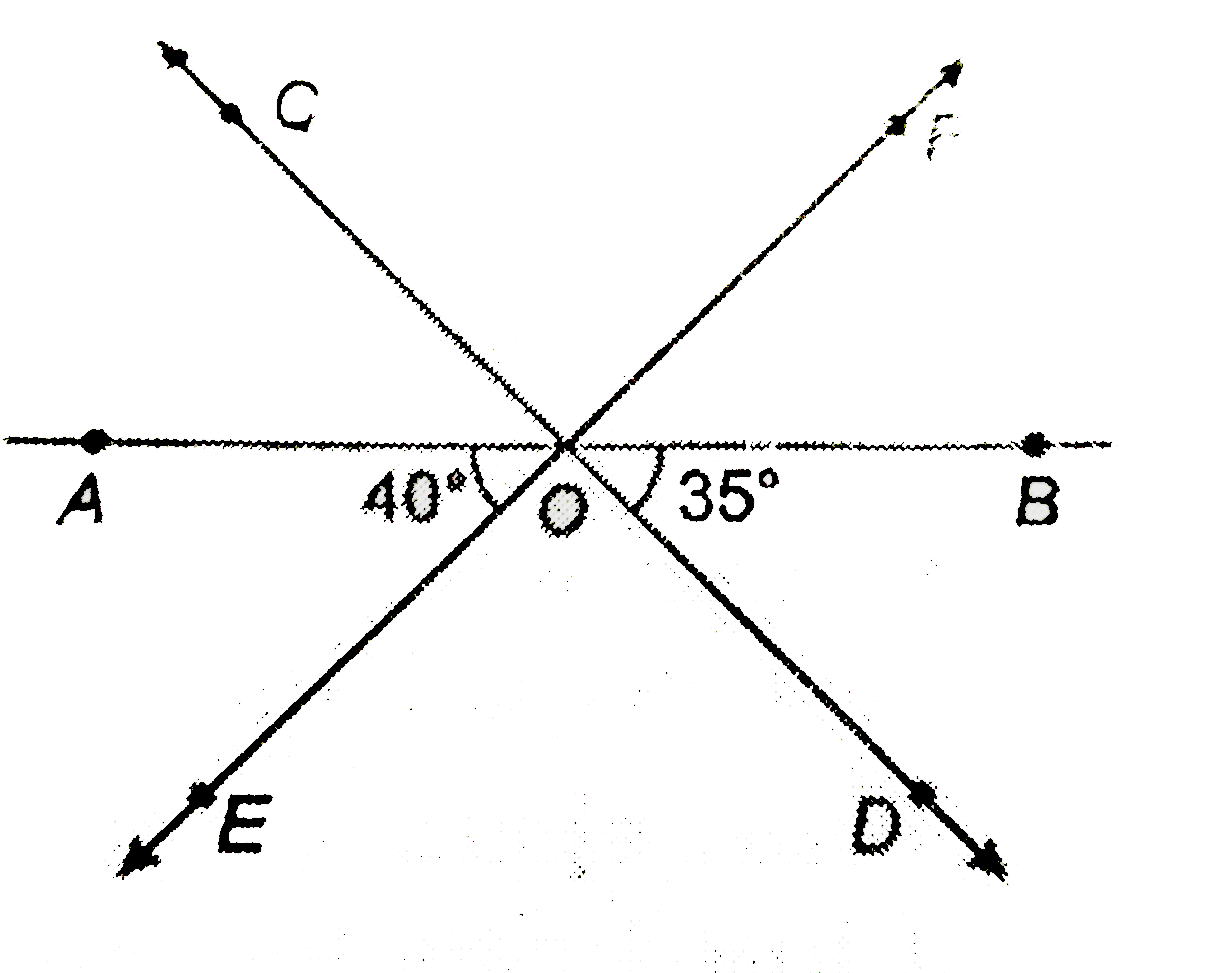
In the given figure, find the measures of ∠AOC,∠COF,∠DOEand∠BOF.
View SolutionIn Figure, given that AB∣∣CD If the ratio of the measures of ∠3 and ∠8 is 4:5, find the measures of ∠3 and ∠8.
View SolutionIn Figure, given that AB∣∣CD If the complement of ∠5 equals the supplement of ∠4, find the measures of ∠4 and ∠5.
View SolutionThe adjacent figure PQRS is a trapezium in which SP∣∣RQ, find the measures of ∠P and ∠R.
View SolutionIn Figure, given that AB∣∣CD. If ∠1=(120−x)∘and ∠5=5x∘, find the measures of ∠1 and ∠5.
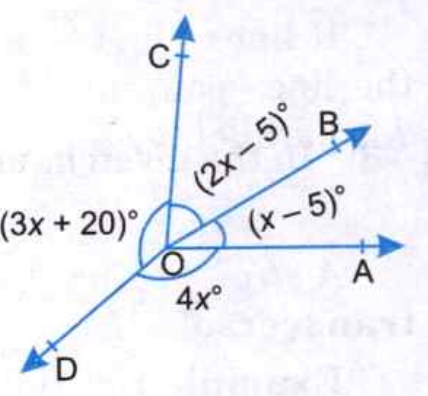
View SolutionIn the given figure, find the value of x. What is the measure of ∠COD?
View SolutionIn Figure, BD=DC and ∠DBC=250 find the measure of ∠BAC
View Solution
