In a parallelogram the sum of any two adjacent angles is 1800.
To prove that in a parallelogram the sum of any two adjacent angles is 180∘, we can follow these steps:
Step 1: Draw a Parallelogram
Let's start by drawing a parallelogram ABCD.
Step 2: Identify Adjacent Angles
Identify two adjacent angles. For example, we can take angle A and angle B.
Step 3: Use Properties of Parallel Lines
In a parallelogram, opposite sides are parallel. Therefore, AB∥CD and AD∥BC.
Step 4: Identify the Transversal
Since AD acts as a transversal line intersecting the parallel lines AB and CD, we can apply the properties of angles formed by a transversal.
Step 5: Apply the Consecutive Interior Angles Theorem
According to the Consecutive Interior Angles Theorem, the sum of the angles on the same side of the transversal is 180∘. Therefore, we can write:
∠A+∠D=180∘
Step 6: Repeat for Other Angles
Similarly, we can consider the transversal AB intersecting the parallel lines AD and BC. Thus, we have:
∠A+∠B=180∘
Step 7: Conclusion
We can conclude that the sum of any two adjacent angles in a parallelogram is 180∘.
Let's start by drawing a parallelogram ABCD.
Identify two adjacent angles. For example, we can take angle A and angle B.
In a parallelogram, opposite sides are parallel. Therefore, AB∥CD and AD∥BC.
Since AD acts as a transversal line intersecting the parallel lines AB and CD, we can apply the properties of angles formed by a transversal.
According to the Consecutive Interior Angles Theorem, the sum of the angles on the same side of the transversal is 180∘. Therefore, we can write:
Similarly, we can consider the transversal AB intersecting the parallel lines AD and BC. Thus, we have:
We can conclude that the sum of any two adjacent angles in a parallelogram is 180∘.
Topper's Solved these Questions
Similar Questions
In a parallelogram; the bisectors of any two consecutive angles intersect at right angle.
View Solution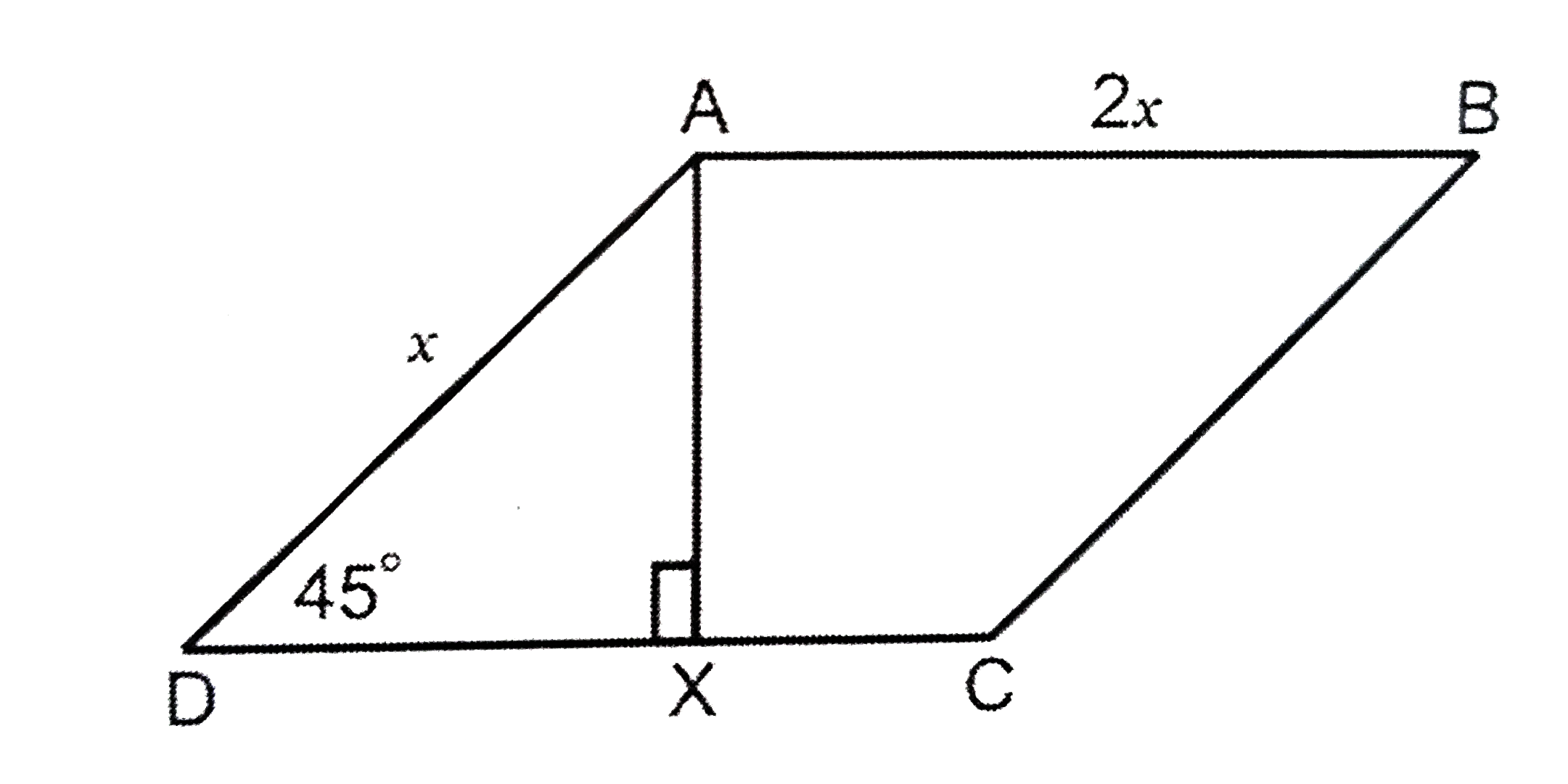
In a parallelogram, the ratio of the two adjacent sides is 1 : 2. If the area of the parallelogram is 20 square units and the angle beween the two sides is 45∘, what is the area, to the nearest integer, of the rectangle having the sides equal to that of the parallelogram?
View SolutionIn a parallelogram ABCD, prove that sum of any two consecutive angles is 1800.
View SolutionIn a parallelogram, two adjacent angles are supplementary.
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionIf an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
View SolutionIf an angle of a parallelogram is two-third of its adjacent angle, find the smallest angle of the parallelogram.
View SolutionIf an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
View SolutionProve that in any parallelogram the sum of squares of the diagonals is twice the sum of the squares of two adjascent sides. Also show that the difference of the squares on two adjacent sides is equal to the rectangle contained by either diagonal and the projection of the other upon it.
View SolutionIn a parallelogram ABCD , write the sum of angle A and B
View Solution
