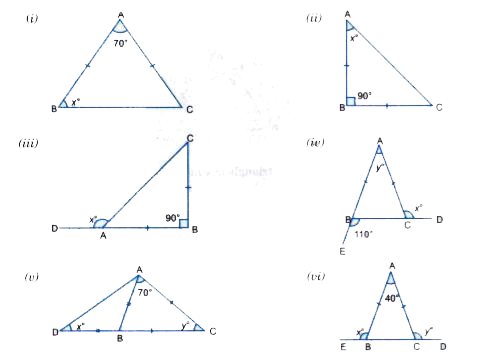
Find the angles marked with a question mark shown in Figure:
To find the angles marked with a question mark in the given figure, we will follow these steps:
Step 1: Analyze Triangle CEB
In triangle CEB, we know that the sum of all interior angles is 180 degrees. The angles in triangle CEB are:
- Angle CEB = 90 degrees (given)
- Angle EBC = ? (marked with a question mark)
- Angle BCE = 40 degrees (given)
Using the angle sum property of triangles:
Angle CEB+Angle EBC+Angle BCE=180∘
Substituting the known values:
90∘+Angle EBC+40∘=180∘
This simplifies to:
Angle EBC+130∘=180∘
Now, subtract 130 degrees from both sides:
Angle EBC=180∘−130∘=50∘
Step 2: Find Angle ADC
Since CEB is a parallelogram, the opposite angles are equal. Therefore:
Angle ADC=Angle EBC=50∘
Step 3: Analyze Triangle FDC
In triangle FDC, we again use the angle sum property:
Angle FDC+Angle CFD+Angle FCD=180∘
We know:
- Angle FDC = 50 degrees (calculated from the previous step)
- Angle CFD = 90 degrees (given)
Substituting these values:
50∘+90∘+Angle FCD=180∘
This simplifies to:
140∘+Angle FCD=180∘
Subtracting 140 degrees from both sides gives:
Angle FCD=180∘−140∘=40∘
Step 4: Find Angle ECF
Now, we know:
- Angle ECD = 90 degrees (as it is opposite to angle CEB)
- Angle FCD = 40 degrees (calculated above)
Using the angle sum property in triangle ECF:
Angle ECF+Angle FCD=90∘
Substituting the known value of Angle FCD:
Angle ECF+40∘=90∘
Subtracting 40 degrees from both sides gives:
Angle ECF=90∘−40∘=50∘
Summary of Angles
- Angle EBC = 50 degrees
- Angle ADC = 50 degrees
- Angle ECF = 50 degrees
In triangle CEB, we know that the sum of all interior angles is 180 degrees. The angles in triangle CEB are:
- Angle CEB = 90 degrees (given)
- Angle EBC = ? (marked with a question mark)
- Angle BCE = 40 degrees (given)
Angle CEB+Angle EBC+Angle BCE=180∘
Substituting the known values:
90∘+Angle EBC+40∘=180∘
This simplifies to:
Angle EBC+130∘=180∘
Now, subtract 130 degrees from both sides:
Angle EBC=180∘−130∘=50∘
Since CEB is a parallelogram, the opposite angles are equal. Therefore:
Angle ADC=Angle EBC=50∘
In triangle FDC, we again use the angle sum property:
Angle FDC+Angle CFD+Angle FCD=180∘
We know:
- Angle FDC = 50 degrees (calculated from the previous step)
- Angle CFD = 90 degrees (given)
50∘+90∘+Angle FCD=180∘
This simplifies to:
140∘+Angle FCD=180∘
Subtracting 140 degrees from both sides gives:
Angle FCD=180∘−140∘=40∘
Now, we know:
- Angle ECD = 90 degrees (as it is opposite to angle CEB)
- Angle FCD = 40 degrees (calculated above)
Angle ECF+Angle FCD=90∘
Substituting the known value of Angle FCD:
Angle ECF+40∘=90∘
Subtracting 40 degrees from both sides gives:
Angle ECF=90∘−40∘=50∘
- Angle EBC = 50 degrees
- Angle ADC = 50 degrees
- Angle ECF = 50 degrees
Topper's Solved these Questions
Similar Questions
Knowledge Check
In series LCR circuit, the plot of Imax versus ω is shown in figure. Find the bandwith and mark in the figure.
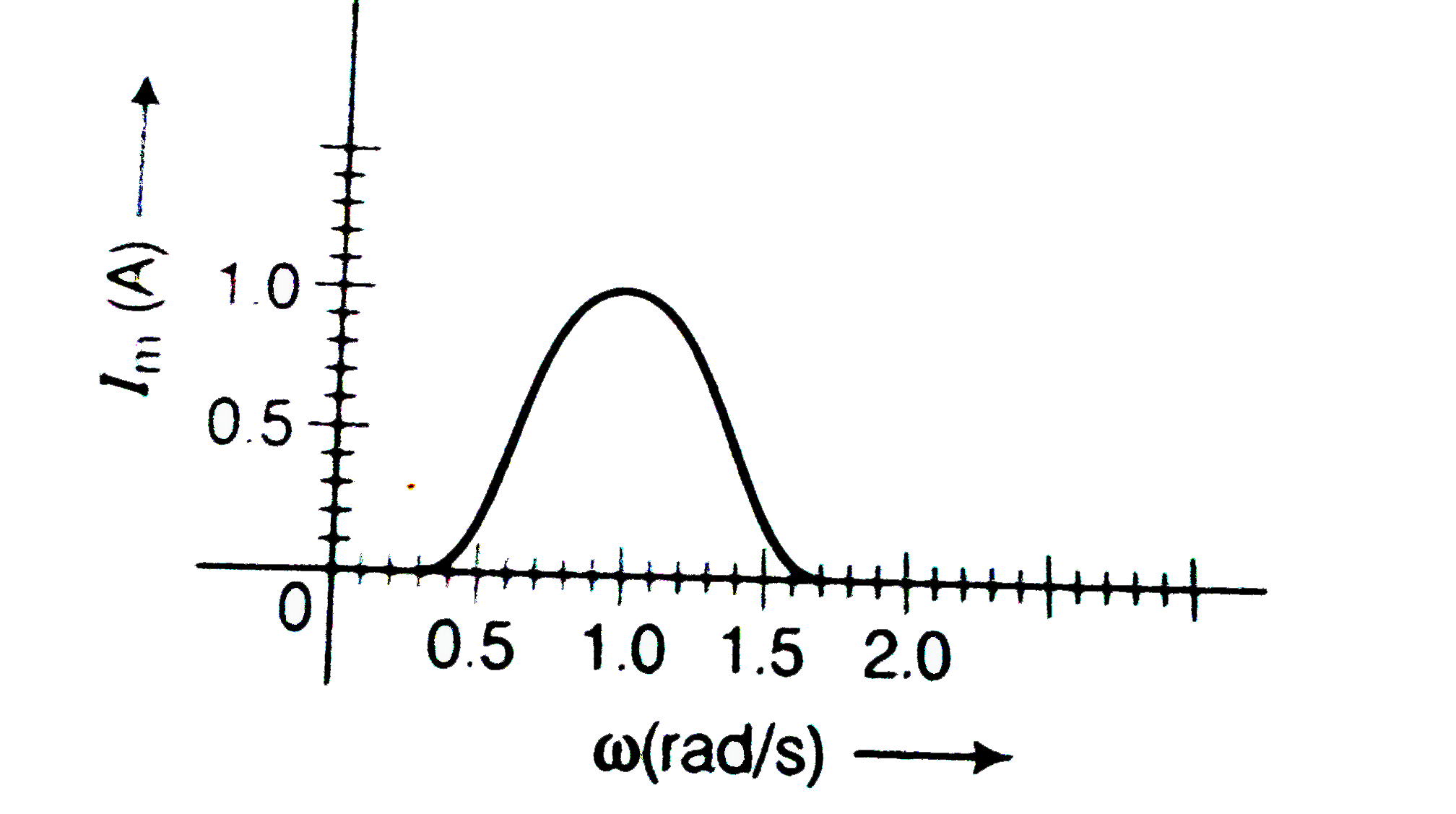 AzeroB0.1rad s−1C0.2rad s−1D0.4rad s−1
AzeroB0.1rad s−1C0.2rad s−1D0.4rad s−1
Observe the figure and answer the question.

Mark i
View SolutionObserve the figure and answer the question.
Mark r
View SolutionThe following table gives the marks of 5 students in Science and Maths.

Find the mean, median, and mode of the marks scored in Science
View SolutionIn Fig. 48, line l ∣∣ line m, n is transversal and ∠1=400. Find all the other angles marked in the figure.
View SolutionA charge particle q is projected in an electric field produced by a fixed point charge Q as shown in figure. Mark the correct statements.

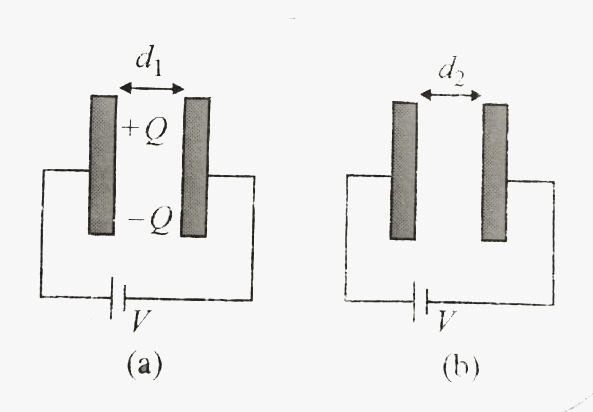
View SolutionConsider a capacitor as shown in figure. If we pull the plates of capacitor apart to a final position as shown in figure, then we must perform some work against the electric force. For this situation, mark out the correct statements.
View SolutionIn series LCR circuit, the plot of Imax versus ω is shown in figure. Find the bandwith and mark in the figure.

View Solution