Length of the fence of a trapezium shaped field ABCD is 120m. If BC=48m,CD=17mandAD=40m, find the area of this field. Side AB is perpendicular to the parallel sides ADandBC.
To find the area of the trapezium-shaped field ABCD, we will follow these steps:
Step 1: Identify the given dimensions
- The lengths of the sides are:
- BC=48m
- CD=17m
- AD=40m
- The total length of the fence (perimeter) is 120m.
Step 2: Set up the perimeter equation
The perimeter of trapezium ABCD can be expressed as:
AB+BC+CD+DA=120m
Substituting the known values:
AB+48+17+40=120
Step 3: Simplify the equation
Combine the known lengths:
AB+105=120
Step 4: Solve for AB
Subtract 105 from both sides to find AB:
AB=120−105=15m
Step 5: Calculate the area of the trapezium
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height (which is AB in this case).
Here, the parallel sides are:
- AD=40m
- BC=48m
Substituting the values into the area formula:
A=12×(40+48)×15
Step 6: Simplify the area calculation
Calculate the sum of the parallel sides:
A=12×88×15
Now, calculate:
A=44×15
Step 7: Final calculation
Now, perform the multiplication:
A=660m2
Thus, the area of the trapezium-shaped field ABCD is 660m2.
---
- The lengths of the sides are:
- BC=48m
- CD=17m
- AD=40m
- The total length of the fence (perimeter) is 120m.
The perimeter of trapezium ABCD can be expressed as:
AB+BC+CD+DA=120m
Substituting the known values:
AB+48+17+40=120
Combine the known lengths:
AB+105=120
Subtract 105 from both sides to find AB:
AB=120−105=15m
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height (which is AB in this case).
- AD=40m
- BC=48m
A=12×(40+48)×15
Calculate the sum of the parallel sides:
A=12×88×15
Now, calculate:
A=44×15
Now, perform the multiplication:
A=660m2
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBOOK - RD SHARMA ENGLISHCHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions
110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions
134 Videos
Similar Questions
The area of a trapezium shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.
View SolutionThe area of a trapezium shaped field is 480 m^2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.
View SolutionThe area of a trapezium shaped field is 1920m2, the height is 30 and one of the parallel sides is 40 m. Find the other parallel side.
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

View SolutionIn the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
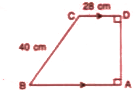
(iii) the area of the trapezium.
View SolutionA field is in the shape of a trapezium whose parallel sides are 25m and 10 m. The non-parallel sides are 14m and 13m. Find the area of the field.
View SolutionA field is in the shape of a trapezium whose parallel sides are 25m and 10 m. The non-parallel sides are 14m and 13m. Find the area of the field.
View SolutionMohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
View SolutionMohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
View SolutionConstruct a trapezium ABCD, when :
AB=CD=3.2cm,BC=6.0cm,AD=4.4cmandAD/BC.
View Solution
