Find the area of Figure, as the sum of the area of two trapezium and a rectangle.
To find the area of the figure, which consists of two trapeziums and a rectangle, we will follow these steps:
Step 1: Identify the dimensions
- The lengths of the parallel sides of the trapeziums are 30 cm and 10 cm.
- The height between the two parallel sides of the trapeziums is 70 cm.
- The length of the rectangle is 50 cm, and we will assume the breadth is equal to the height of the rectangle.
Step 2: Calculate the height of the trapeziums
- The total height between the trapeziums is 70 cm, and the rectangle has a height of 50 cm.
- Therefore, the remaining height for the trapeziums is:
Remaining height=70 cm−50 cm=20 cm
- Since there are two trapeziums, we divide this height by 2 to find the height of each trapezium:
Height of each trapezium=20 cm2=10 cm
Step 3: Calculate the area of one trapezium
- The formula for the area of a trapezium is:
Area=12×(Sum of parallel sides)×Height
- For one trapezium, substituting the values:
Area of one trapezium=12×(30 cm+10 cm)×10 cm
=12×40 cm×10 cm=200 cm2
Step 4: Calculate the area of two trapeziums
- Since there are two trapeziums:
Area of two trapeziums=2×200 cm2=400 cm2
Step 5: Calculate the area of the rectangle
- The area of the rectangle is given by:
Area of rectangle=Length×Breadth
- Assuming the breadth of the rectangle is equal to the height of the rectangle (50 cm):
Area of rectangle=50 cm×10 cm=500 cm2
Step 6: Calculate the total area
- Now, we add the area of the two trapeziums and the area of the rectangle:
Total Area=Area of two trapeziums+Area of rectangle
=400 cm2+500 cm2=900 cm2
Final Answer
The total area of the figure is 900 cm2.
---
- The lengths of the parallel sides of the trapeziums are 30 cm and 10 cm.
- The height between the two parallel sides of the trapeziums is 70 cm.
- The length of the rectangle is 50 cm, and we will assume the breadth is equal to the height of the rectangle.
- The total height between the trapeziums is 70 cm, and the rectangle has a height of 50 cm.
- Therefore, the remaining height for the trapeziums is:
Remaining height=70 cm−50 cm=20 cm
- Since there are two trapeziums, we divide this height by 2 to find the height of each trapezium:
Height of each trapezium=20 cm2=10 cm
- The formula for the area of a trapezium is:
Area=12×(Sum of parallel sides)×Height
- For one trapezium, substituting the values:
Area of one trapezium=12×(30 cm+10 cm)×10 cm
=12×40 cm×10 cm=200 cm2
- Since there are two trapeziums:
Area of two trapeziums=2×200 cm2=400 cm2
- The area of the rectangle is given by:
Area of rectangle=Length×Breadth
- Assuming the breadth of the rectangle is equal to the height of the rectangle (50 cm):
Area of rectangle=50 cm×10 cm=500 cm2
- Now, we add the area of the two trapeziums and the area of the rectangle:
Total Area=Area of two trapeziums+Area of rectangle
=400 cm2+500 cm2=900 cm2
The total area of the figure is 900 cm2.
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBOOK - RD SHARMA ENGLISHCHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions
110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions
134 Videos
Similar Questions
Find the area of a trapezium whose parallel sides of lengths 10cm and 15cm are at a distance of 6cm from each other. Calculate this area as (a) the sum of the areas of two triangles and one rectangle. (b) the difference of the area of a rectangle and the sum of the areas of two triangles.
View SolutionFind the area of trapezium in the given figure.
View Solution
Knowledge Check
The figure above shows the graph of 5x . What is the sum of the areas of the rectangle ?
A32550B16225C2604D651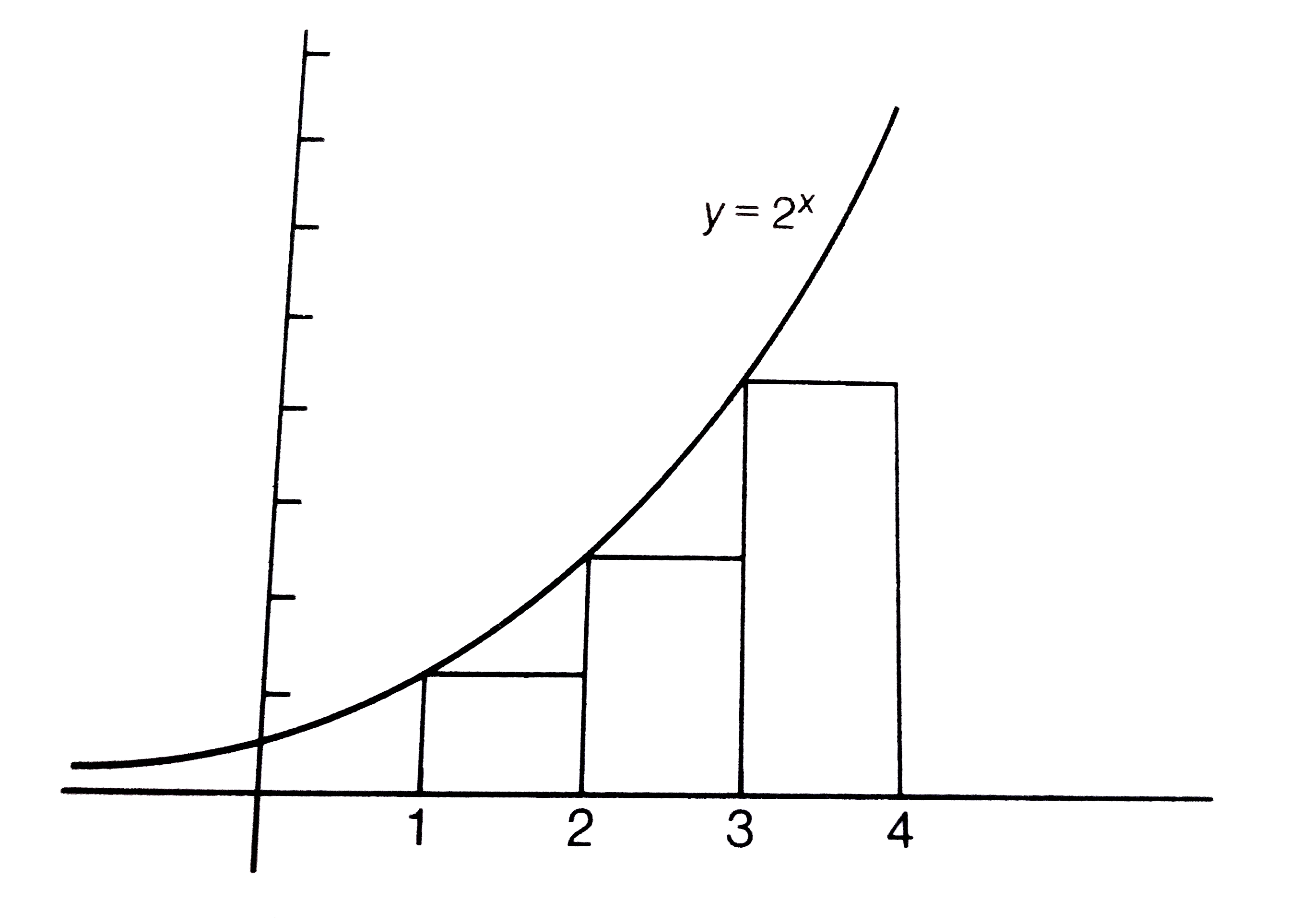
The figure above shows a portion of the graph of y=2x. What is the sum of the areas of the three inscribed rectangles shown?A14B28C128D256
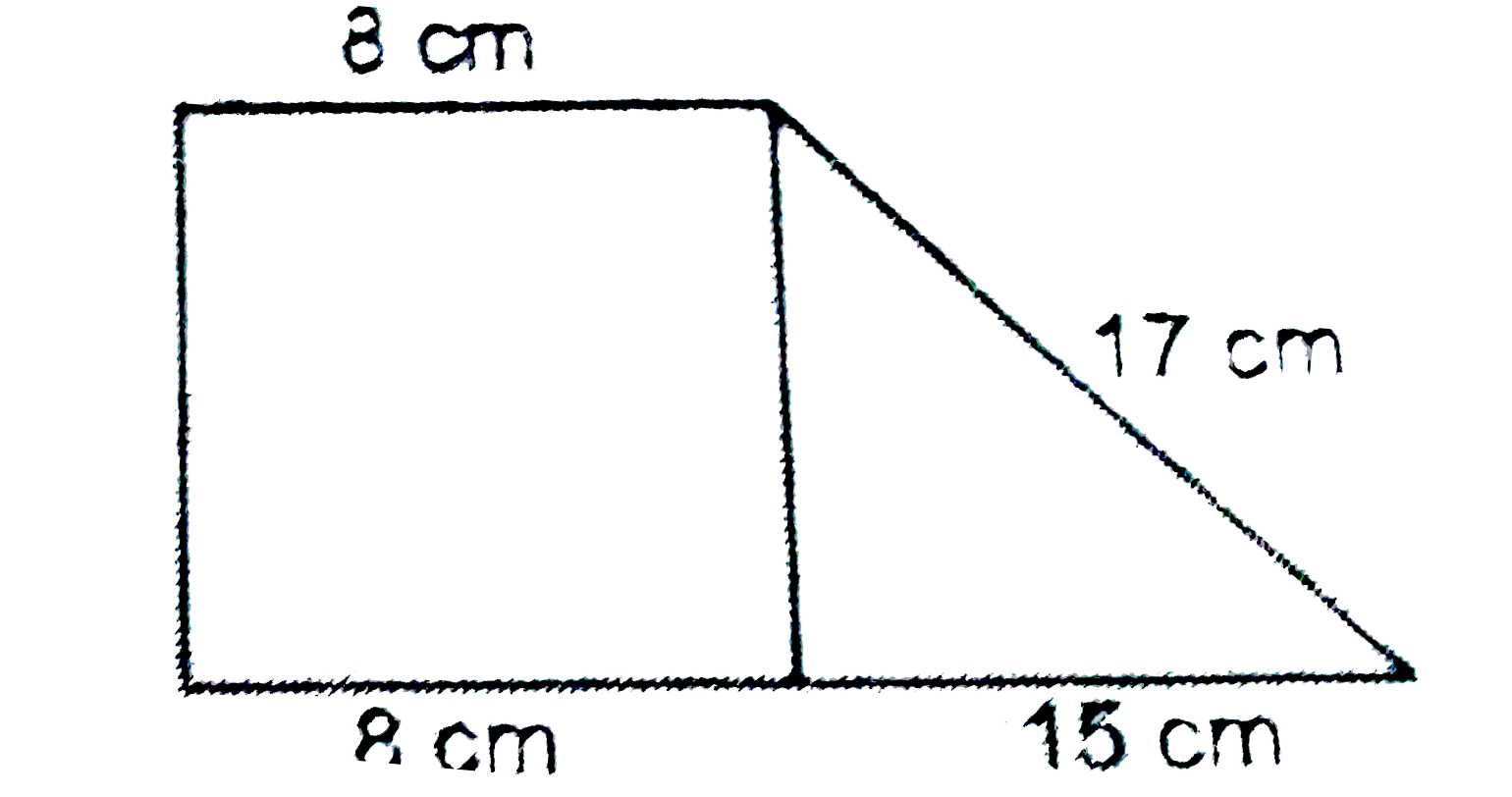
Find the area of the given trapezium.
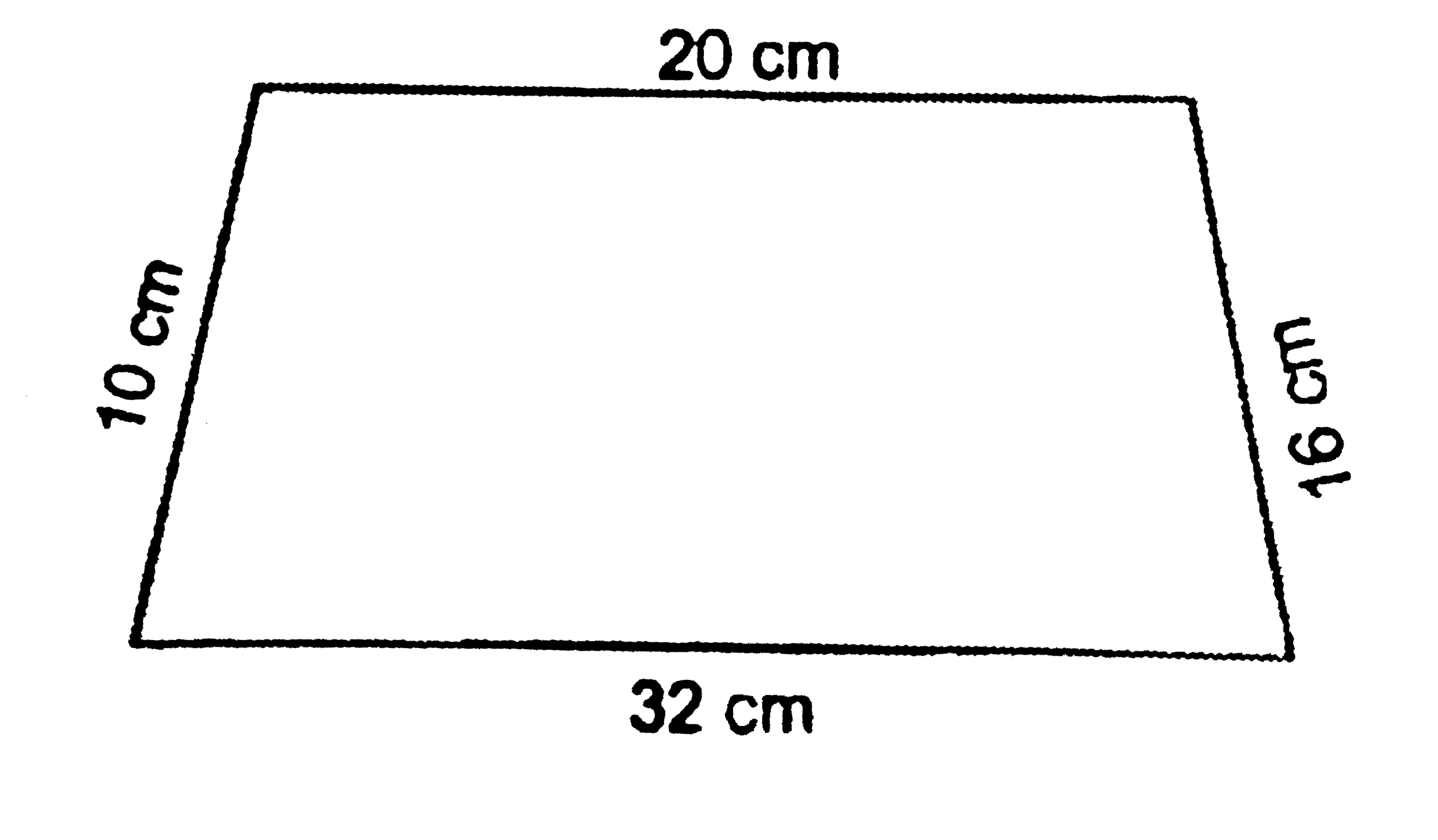
View SolutionFind the area of the given figure.
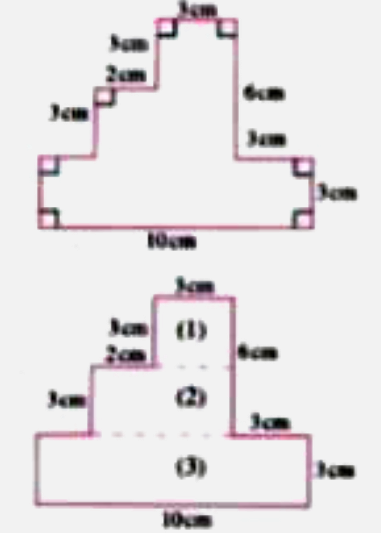
View SolutionFind the area of the given figure.
View SolutionFind the area of the trapezium given in given figure.
View SolutionThe side of a rectangle is 6 more than its breadth. If the breadth is a, find the rule for finding the area of the rectangle. If the breadth of the rectangle is 8 cm, find its area.
View SolutionIn the given figure, find the area of the unshaded portion within the rectangle. (Take π=3.14).

View Solution
