Question

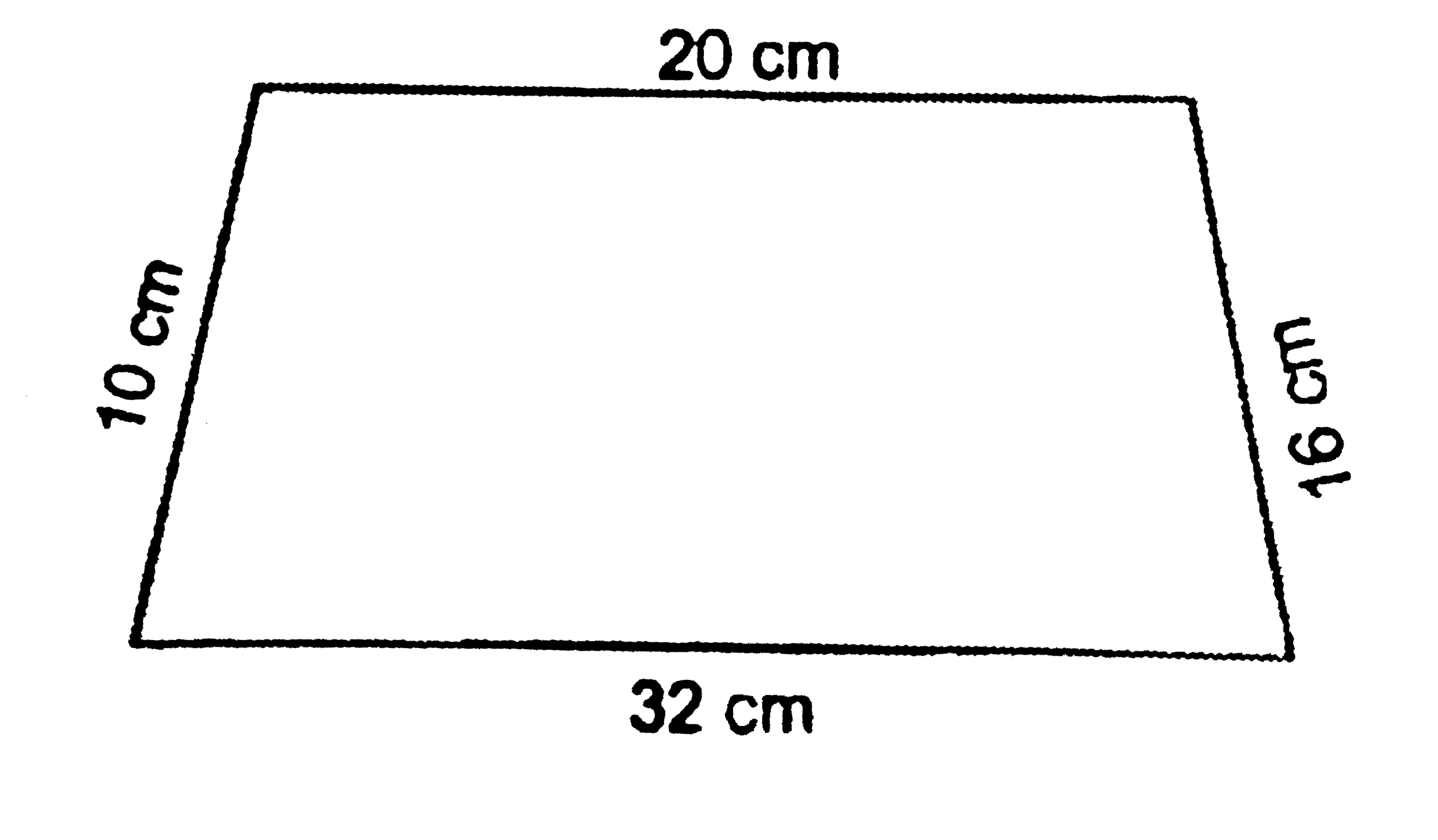
In Figure, a parallelogram is drawn in a
trapezium, the area of the parallelogram is $80c{m}^2,$
find the area of the trapezium.

Explanation

To find the area of the trapezium given that the area of the parallelogram is $$80c{m}^2$$, we can follow these steps:

1. Identify the Given Information:
- Area of the parallelogram \( = 80 \, cm^2\).
- Let the base of the parallelogram \( = a = 10 \, cm\).
- Let the height of the parallelogram (which is also the height of the trapezium) \( = d_f\).

2. Use the Area Formula for the Parallelogram:
- The area of a parallelogram is given by the formula:
\( \text{Area} = \text{Base} \times \text{Height} \)
- Substituting the known values:
\( 80 = 10 \times d_f \)

3. Calculate the Height \(d_f\):
- Rearranging the equation to find \(d_f\):
\( d_f = \frac{80}{10} = 8 \, cm \)

4. Identify the Parallel Sides of the Trapezium:
- Let the lengths of the parallel sides of the trapezium be \(AB = 22 \, cm\) and \(CD = 10 \, cm\).

5. Use the Area Formula for the Trapezium:
- The area of a trapezium is given by the formula:
\( \text{Area} = \frac{1}{2} \times (\text{Base}_1 + \text{Base}_2) \times \text{Height} \)
- Substituting the values:
\( \text{Area} = \frac{1}{2} \times (22 + 10) \times 8 \)

6. Calculate the Area of the Trapezium:
- First, calculate the sum of the bases:
\( 22 + 10 = 32 \)
- Now substitute back into the area formula:
\( \text{Area} = \frac{1}{2} \times 32 \times 8 \)
- Calculate:
\( \text{Area} = 16 \times 8 = 128 \, cm^2 \)

7. Final Answer:
- Therefore, the area of the trapezium is \(128 \, cm^2\).