There is a regular hexagon MNOPQR of side 5 cm . aman and ridhima divided it into two different ways . Find the area of this hexagon both ways.
To find the area of the regular hexagon MNOPQR with a side length of 5 cm using two different methods, we can follow these steps:
Method 1: Ridhima's Method
1. Identify the Shape and Divide:
- The hexagon can be divided into a rectangle (MOPR) and two triangles (MNO and RQP).
2. Calculate the Area of the Rectangle:
- The rectangle MOPR has a length equal to the distance between points M and O (which is 8 cm) and a height equal to the side of the hexagon (5 cm).
- Area of Rectangle = Length × Height = 8 cm × 5 cm = 40 cm².
3. Calculate the Height of the Triangles:
- The total height of the hexagon is 11 cm.
- The height of each triangle can be calculated as follows:
- Total height = 11 cm
- Subtract the height of the rectangle (5 cm), so the remaining height = 11 cm - 5 cm = 6 cm.
- Since there are two triangles, the height of each triangle (h) = 6 cm / 2 = 3 cm.
4. Calculate the Area of One Triangle:
- The base of triangle MNO is equal to the side of the hexagon (5 cm).
- Area of Triangle = 1/2 × Base × Height = 1/2 × 5 cm × 3 cm = 7.5 cm².
5. Calculate the Total Area of the Hexagon:
- Total Area = Area of Rectangle + Area of Triangle MNO + Area of Triangle RQP
- Total Area = 40 cm² + 7.5 cm² + 7.5 cm² = 55 cm².
Method 2: Aman’s Method
1. Identify the Shape and Divide:
- The hexagon can be divided into two trapeziums: trapezium NO PQ and trapezium NMRQ.
2. Calculate the Area of One Trapezium:
- The area of a trapezium is given by the formula:
Area=12×(Sum of parallel sides)×Height
- For trapezium NO PQ, the parallel sides are PQ (11 cm) and NQ (5 cm).
- The height (x) can be calculated as half of the rectangle’s height, which is 4 cm.
3. Calculate the Area of Trapezium NO PQ:
- Area of Trapezium = 1/2 × (11 cm + 5 cm) × 4 cm
- Area = 1/2 × 16 cm × 4 cm = 32 cm².
4. Calculate the Total Area of the Hexagon:
- Since there are two identical trapeziums, the total area is:
- Total Area = 2 × Area of Trapezium NO PQ = 2 × 32 cm² = 64 cm².
Final Area of the Hexagon
- Both methods yield the area of the hexagon MNOPQR as follows:
- Ridhima’s Method: 55 cm²
- Aman’s Method: 64 cm²
- The hexagon can be divided into a rectangle (MOPR) and two triangles (MNO and RQP).
- The rectangle MOPR has a length equal to the distance between points M and O (which is 8 cm) and a height equal to the side of the hexagon (5 cm).
- Area of Rectangle = Length × Height = 8 cm × 5 cm = 40 cm².
- The total height of the hexagon is 11 cm.
- The height of each triangle can be calculated as follows:
- Total height = 11 cm
- Subtract the height of the rectangle (5 cm), so the remaining height = 11 cm - 5 cm = 6 cm.
- Since there are two triangles, the height of each triangle (h) = 6 cm / 2 = 3 cm.
- The base of triangle MNO is equal to the side of the hexagon (5 cm).
- Area of Triangle = 1/2 × Base × Height = 1/2 × 5 cm × 3 cm = 7.5 cm².
- Total Area = Area of Rectangle + Area of Triangle MNO + Area of Triangle RQP
- Total Area = 40 cm² + 7.5 cm² + 7.5 cm² = 55 cm².
- The hexagon can be divided into two trapeziums: trapezium NO PQ and trapezium NMRQ.
- The area of a trapezium is given by the formula:
Area=12×(Sum of parallel sides)×Height
- For trapezium NO PQ, the parallel sides are PQ (11 cm) and NQ (5 cm).
- The height (x) can be calculated as half of the rectangle’s height, which is 4 cm.
- Area of Trapezium = 1/2 × (11 cm + 5 cm) × 4 cm
- Area = 1/2 × 16 cm × 4 cm = 32 cm².
- Since there are two identical trapeziums, the total area is:
- Total Area = 2 × Area of Trapezium NO PQ = 2 × 32 cm² = 64 cm².
- Both methods yield the area of the hexagon MNOPQR as follows:
- Ridhima’s Method: 55 cm²
- Aman’s Method: 64 cm²
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBOOK - RD SHARMA ENGLISHCHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions
110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions
134 Videos
Similar Questions
Knowledge Check
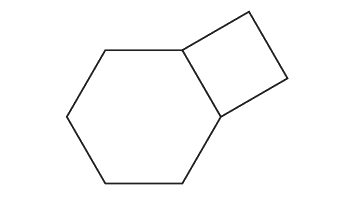
The figure above shows a regular hexagon with sides of length a and a square with sides of length a. If the area of the hexagon is 384 √3 square inches, what is the area, in square inches, of the square?A256B192C64√3D16√3
Construct a regular hexagon of side
(i) 2.5cm
(ii) 3.2cm.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionFind the area of a square whose side is 5cm.
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionDraw a circle circumscribing a regular hexagon with side 5 cm.
View SolutionConstruct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
View Solution
