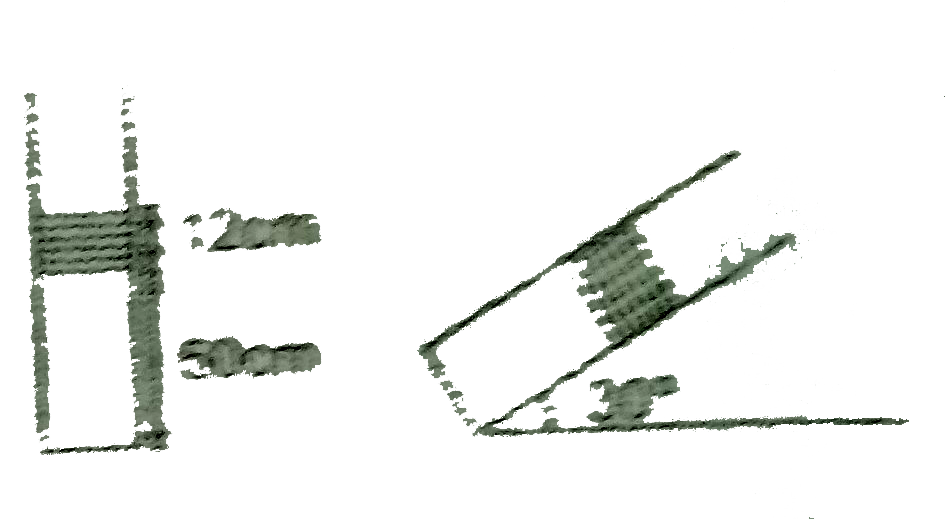
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the cloumn. The upper end of the tube is open to the atmosphere. the atmosphric pressure equals 76cm of mercury. The lenghts of the mercury column respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60∘? Assume the temperature to remain constant.
Case 1 : Atmospheric pressure + Pressure
due to mercury column
Case 2 : Atmospheric pressure +
Component of the pressure due
to mercury column
((P1)(V1)=(P2)(V2))
⇒(76×(ρHg)×g+(ρHg)×g×20)×A×43
=(76×(ρHg)×g+(ρHg)×g
×20×(cos60∘)×A×1
⇒96×43=86×L
⇒L=(96×4386)=48cm.

Topper's Solved these Questions
Similar Questions
An ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
View Solution
Knowledge Check
What will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
In given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)

View SolutionA vertical uniform U tube open at both ends contains mercury. Water is poured in one limb until the level of mercury is depressed 2cm in that limb. What is the length of water column when this happens.
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View Solution
