A particle moves on a given straight line with a constant speed v. At a certain time it is at a point P o its straight lline path.O is a fixed point. Show than −−→OP×→υ is independent of the position P.?
To show that →OP×→v is independent of the position P, we can follow these steps:
Step 1: Define the vectors
Let:
- →OP be the position vector from point O (fixed point) to point P (the position of the particle).
- →v be the velocity vector of the particle, which is constant and directed along the straight line of motion.
Step 2: Analyze the angle between vectors
The angle between the position vector →OP and the velocity vector →v is denoted as θ.
Step 3: Calculate the cross product
The magnitude of the cross product →OP×→v can be expressed as:
|→OP×→v|=|→OP||→v|sin(θ)
where |→OP| is the magnitude of the position vector, |→v| is the magnitude of the velocity vector, and sin(θ) is the sine of the angle between the two vectors.
Step 4: Relate the position vector to a fixed projection
Let OA be the projection of →OP onto the line perpendicular to →v. From the triangle formed by the vectors, we have:
|→OP|sin(θ)=OA
Thus, we can rewrite the cross product as:
|→OP×→v|=|→v|⋅OA
Step 5: Show independence from position P
As the particle moves along the straight line, the angle θ may change, but the projection OA remains constant because it is the same distance from point O to the line of motion. Therefore:
→OP×→v=|→v|⋅OA⋅^n
where ^n is a unit vector perpendicular to both →OP and →v.
Conclusion
Since OA is constant and does not change with the position of P, we conclude that →OP×→v is independent of the position P.
---
Let:
- →OP be the position vector from point O (fixed point) to point P (the position of the particle).
- →v be the velocity vector of the particle, which is constant and directed along the straight line of motion.
The angle between the position vector →OP and the velocity vector →v is denoted as θ.
The magnitude of the cross product →OP×→v can be expressed as:
|→OP×→v|=|→OP||→v|sin(θ)
where |→OP| is the magnitude of the position vector, |→v| is the magnitude of the velocity vector, and sin(θ) is the sine of the angle between the two vectors.
Let OA be the projection of →OP onto the line perpendicular to →v. From the triangle formed by the vectors, we have:
|→OP|sin(θ)=OA
Thus, we can rewrite the cross product as:
|→OP×→v|=|→v|⋅OA
As the particle moves along the straight line, the angle θ may change, but the projection OA remains constant because it is the same distance from point O to the line of motion. Therefore:
→OP×→v=|→v|⋅OA⋅^n
where ^n is a unit vector perpendicular to both →OP and →v.
Since OA is constant and does not change with the position of P, we conclude that →OP×→v is independent of the position P.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 25videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle moves in a straight line and its position x at time t is given by x2=2+t. Its acceleration is given by :-
View SolutionA particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
 View Solution
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant
 View Solution
View SolutionA straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point.
View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
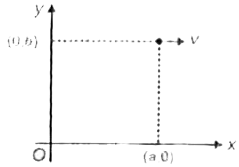 View Solution
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View Solution

