The electric current in a discharging R-C circuit is given by i=i0e−tRC where i0 Rand Care constant parameters and tis time. Let i0=2.00A, R=6.00×105ohm and C=0.500μF.
a. Find the current at t=0.3 s.
b. Find the rate of change of current at t=0.3 s.
Find approximately the current at t=0.31 s.
The correct Answer is:(a)2/e (b)-20/3e (c)5.8/3e
To solve the problem step by step, we will follow the instructions given in the question and use the formula provided for the electric current in a discharging R-C circuit.
Given:
- i0=2.00A
- R=6.00×105Ω
- C=0.500μF=0.500×10−6F
Step 1: Calculate RC
First, we need to calculate the product RC:
RC=R×C=(6.00×105Ω)×(0.500×10−6F)
RC=6.00×0.500×10−1=3.00×10−1=0.3s
Step 2: Find the current at t=0.3s
Using the formula for current:
i=i0e−tRC
Substituting t=0.3s:
i=2.00e−0.30.3=2.00e−1
Calculating e−1:
e−1≈0.3679
Thus,
i≈2.00×0.3679≈0.7358A
Step 3: Find the rate of change of current at t=0.3s
To find the rate of change of current, we differentiate the current with respect to time:
didt=−i0RCe−tRC
Substituting i0=2.00A, RC=0.3s, and t=0.3s:
didt=−2.000.3e−1
Calculating:
didt=−2.000.3×0.3679≈−6.6667×0.3679≈−2.4489A/s
Step 4: Find the current at t=0.31s
Now we calculate the current at t=0.31s:
i=i0e−tRC=2.00e−0.310.3
Calculating e−0.310.3:
e−0.310.3≈e−1.0333≈0.3567
Thus,
i≈2.00×0.3567≈0.7134A
Summary of Results:
a. Current at t=0.3s: ≈0.7358A
b. Rate of change of current at t=0.3s: ≈−2.4489A/s
c. Current at t=0.31s: ≈0.7134A
- i0=2.00A
- R=6.00×105Ω
- C=0.500μF=0.500×10−6F
First, we need to calculate the product RC:
RC=R×C=(6.00×105Ω)×(0.500×10−6F)
RC=6.00×0.500×10−1=3.00×10−1=0.3s
Using the formula for current:
i=i0e−tRC
Substituting t=0.3s:
i=2.00e−0.30.3=2.00e−1
Calculating e−1:
e−1≈0.3679
Thus,
i≈2.00×0.3679≈0.7358A
To find the rate of change of current, we differentiate the current with respect to time:
didt=−i0RCe−tRC
Substituting i0=2.00A, RC=0.3s, and t=0.3s:
didt=−2.000.3e−1
Calculating:
didt=−2.000.3×0.3679≈−6.6667×0.3679≈−2.4489A/s
Now we calculate the current at t=0.31s:
i=i0e−tRC=2.00e−0.310.3
Calculating e−0.310.3:
e−0.310.3≈e−1.0333≈0.3567
Thus,
i≈2.00×0.3567≈0.7134A
a. Current at t=0.3s: ≈0.7358A
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 2
5 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
Similar Questions
The electric curren in a charging R-C circuit is given by i=i0e−tRC when i0, R and C aere constant parameters of the circuit and t is time. Find the rate of change of current at a.t=0,b.t=RCc.t=10RC.
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s is
View SolutionFind the avarage value of current (in A) shown graphically in fig. From t=0→t=2s.
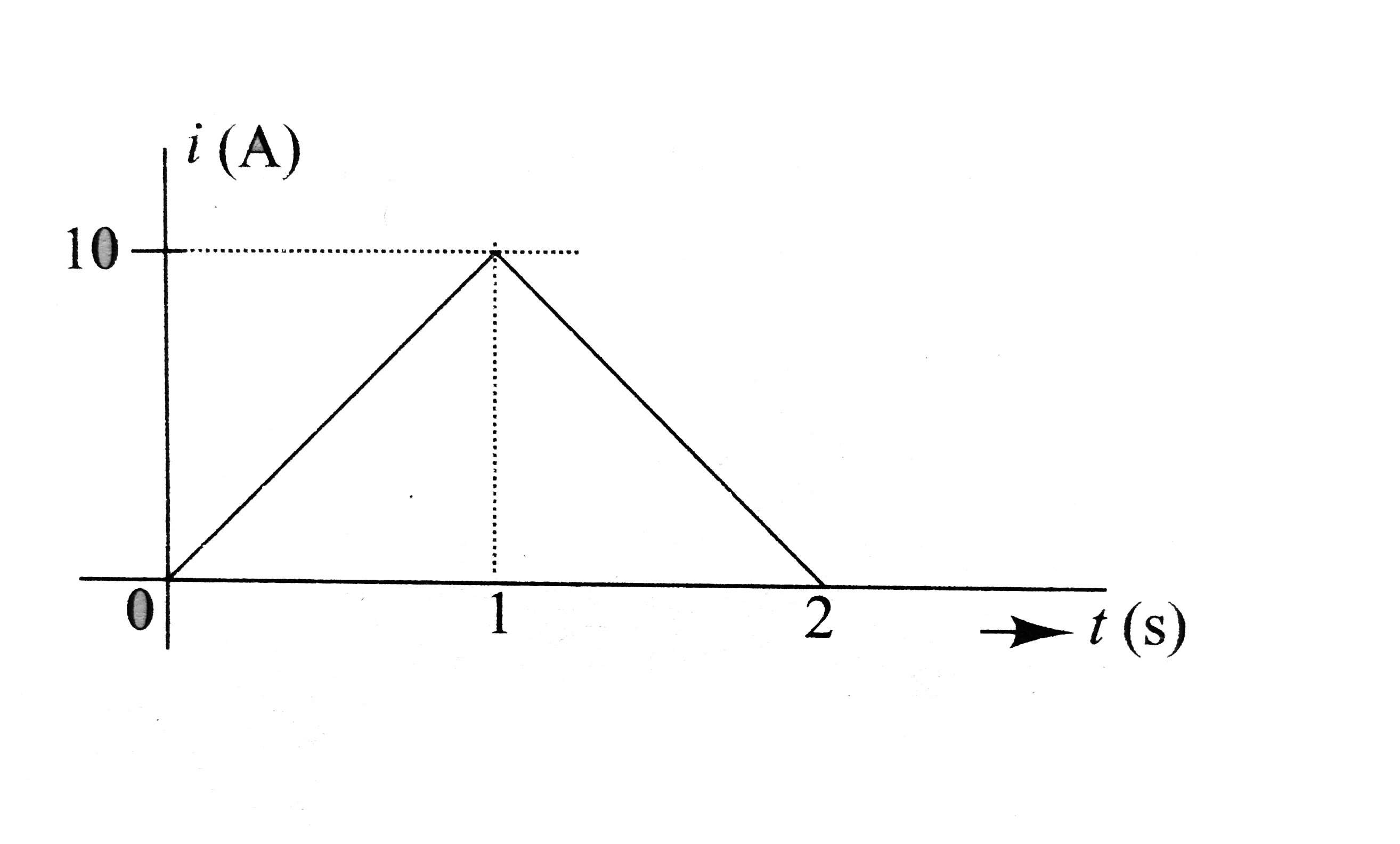 .
.
View SolutionFind the avarage value of current (in A) shown graphically in fig. From t=0→t=2s.
 .
.
View SolutionIf i=t2,0<t<T then r.m.s. value of current is
View SolutionFind the rms value of current from t=0 to t=2πω if the current varies as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View Solution
