Two particles A and B starts from rest and move for equal time on a straight line. The particle A has an acceleration a for the first half of the total time and 2a for the second half. The particle B has an acceleration 2a for the first half and a for the second half. Which particle has covered larger distance?
To solve the problem of which particle, A or B, has covered a larger distance after moving for equal time with different accelerations, we can break down the solution into clear steps.
Step 1: Define the Problem
We have two particles A and B starting from rest and moving for equal time t. Particle A has an acceleration of a for the first half of the time and 2a for the second half. Particle B has an acceleration of 2a for the first half and a for the second half. We need to find the total distance covered by each particle.
Step 2: Calculate Distance for Particle A
1. First Half of Time (0 to t2):
- Initial velocity u=0
- Acceleration a
- Time t1=t2
- Using the formula S=ut+12at2:
S1A=0⋅t2+12a(t2)2=12a⋅t24=at28
2. Second Half of Time (t2 to t):
- Initial velocity u=v1A=a⋅t2
- Acceleration 2a
- Time t2=t2
- Using the same formula:
S2A=v1A⋅t2+12(2a)t22
S2A=(a⋅t2)⋅t2+12(2a)(t2)2
S2A=at24+12(2a)⋅t24=at24+at24=at22
3. Total Distance for Particle A:
SA=S1A+S2A=at28+at22=at28+4at28=5at28
Step 3: Calculate Distance for Particle B
1. First Half of Time (0 to t2):
- Initial velocity u=0
- Acceleration 2a
- Time t1=t2
- Using the formula:
S1B=0⋅t2+12(2a)(t2)2=12(2a)⋅t24=at24
2. Second Half of Time (t2 to t):
- Initial velocity u=v1B=2a⋅t2=at
- Acceleration a
- Time t2=t2
- Using the formula:
S2B=at⋅t2+12a(t2)2
S2B=at⋅t2+12a⋅t24=at22+at28=4at28+at28=5at28
3. Total Distance for Particle B:
SB=S1B+S2B=at24+5at28=2at28+5at28=7at28
Step 4: Compare Distances
Now we can compare the distances:
- Distance covered by Particle A: SA=5at28
- Distance covered by Particle B: SB=7at28
Conclusion
Since SB>SA, Particle B has covered a larger distance than Particle A.
---
We have two particles A and B starting from rest and moving for equal time t. Particle A has an acceleration of a for the first half of the time and 2a for the second half. Particle B has an acceleration of 2a for the first half and a for the second half. We need to find the total distance covered by each particle.
1. First Half of Time (0 to t2):
- Initial velocity u=0
- Acceleration a
- Time t1=t2
- Using the formula S=ut+12at2:
S1A=0⋅t2+12a(t2)2=12a⋅t24=at28
- Initial velocity u=v1A=a⋅t2
- Acceleration 2a
- Time t2=t2
- Using the same formula:
S2A=v1A⋅t2+12(2a)t22
S2A=(a⋅t2)⋅t2+12(2a)(t2)2
S2A=at24+12(2a)⋅t24=at24+at24=at22
SA=S1A+S2A=at28+at22=at28+4at28=5at28
1. First Half of Time (0 to t2):
- Initial velocity u=0
- Acceleration 2a
- Time t1=t2
- Using the formula:
S1B=0⋅t2+12(2a)(t2)2=12(2a)⋅t24=at24
- Initial velocity u=v1B=2a⋅t2=at
- Acceleration a
- Time t2=t2
- Using the formula:
S2B=at⋅t2+12a(t2)2
S2B=at⋅t2+12a⋅t24=at22+at28=4at28+at28=5at28
SB=S1B+S2B=at24+5at28=2at28+5at28=7at28
Now we can compare the distances:
- Distance covered by Particle A: SA=5at28
- Distance covered by Particle B: SB=7at28
Since SB>SA, Particle B has covered a larger distance than Particle A.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Exercises
Explore 51 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Question for short Answer
Explore 14 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
Similar Questions
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
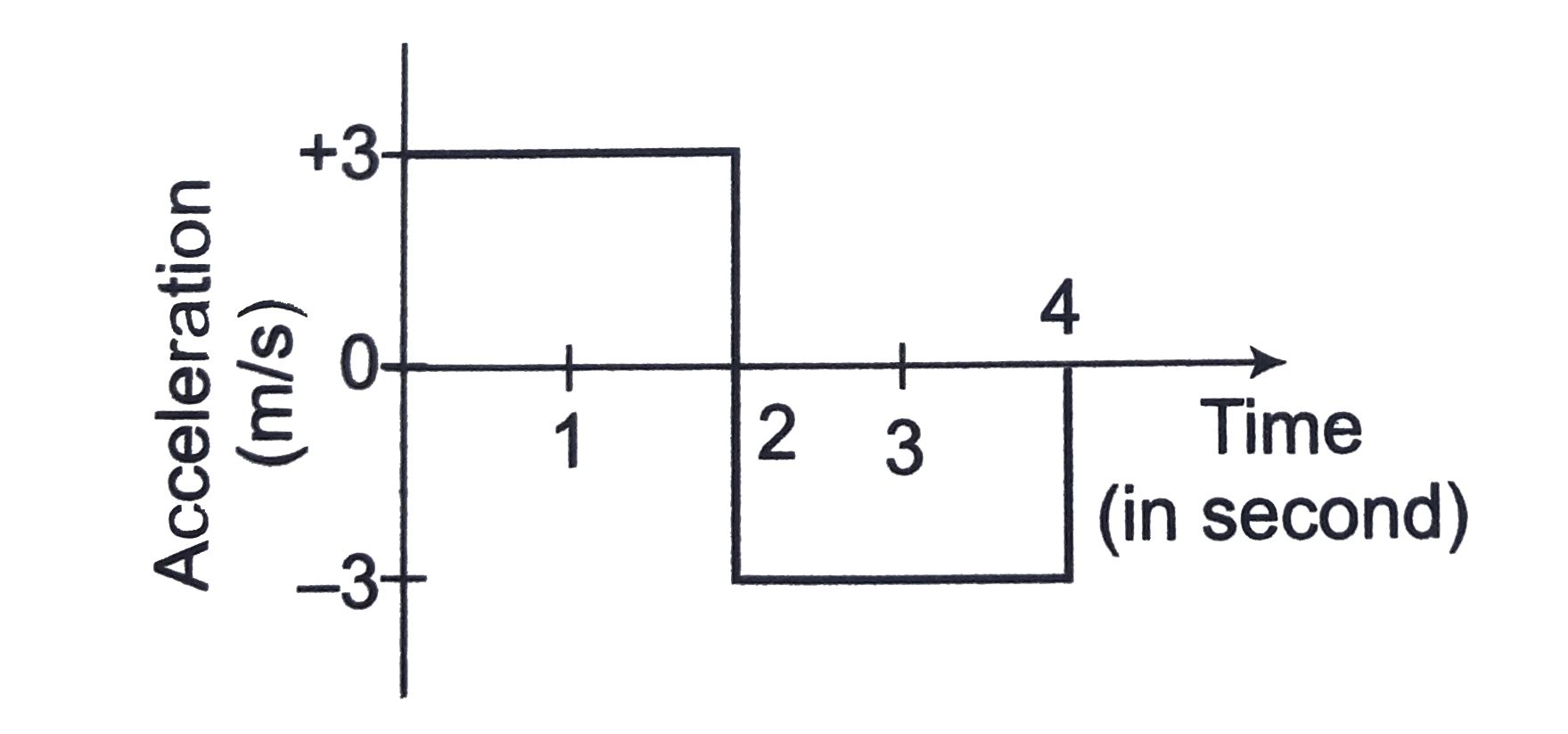
View SolutionA particle starts from rest at time t=0 and moves on a straight line with acceleration as plotted in fig. The speed of the particle will be maximum after time.

View Solution
Knowledge Check
A body starts from rest and moves with constant acceleration for t s. It travels a distance x1 in first half of time and x2 in next half of time, then
Ax2=3x1Bx2=x1Cx2=4x1Dx2=2x1A body starts from rest and travels with uniform acceleration the time taken by the body to cover the whole distance is t. Then the time taken the body to cover the second half of the distance is
At√2Bt(1−1√2)Ct(1+1√2)Dt(1√2−1)
A particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
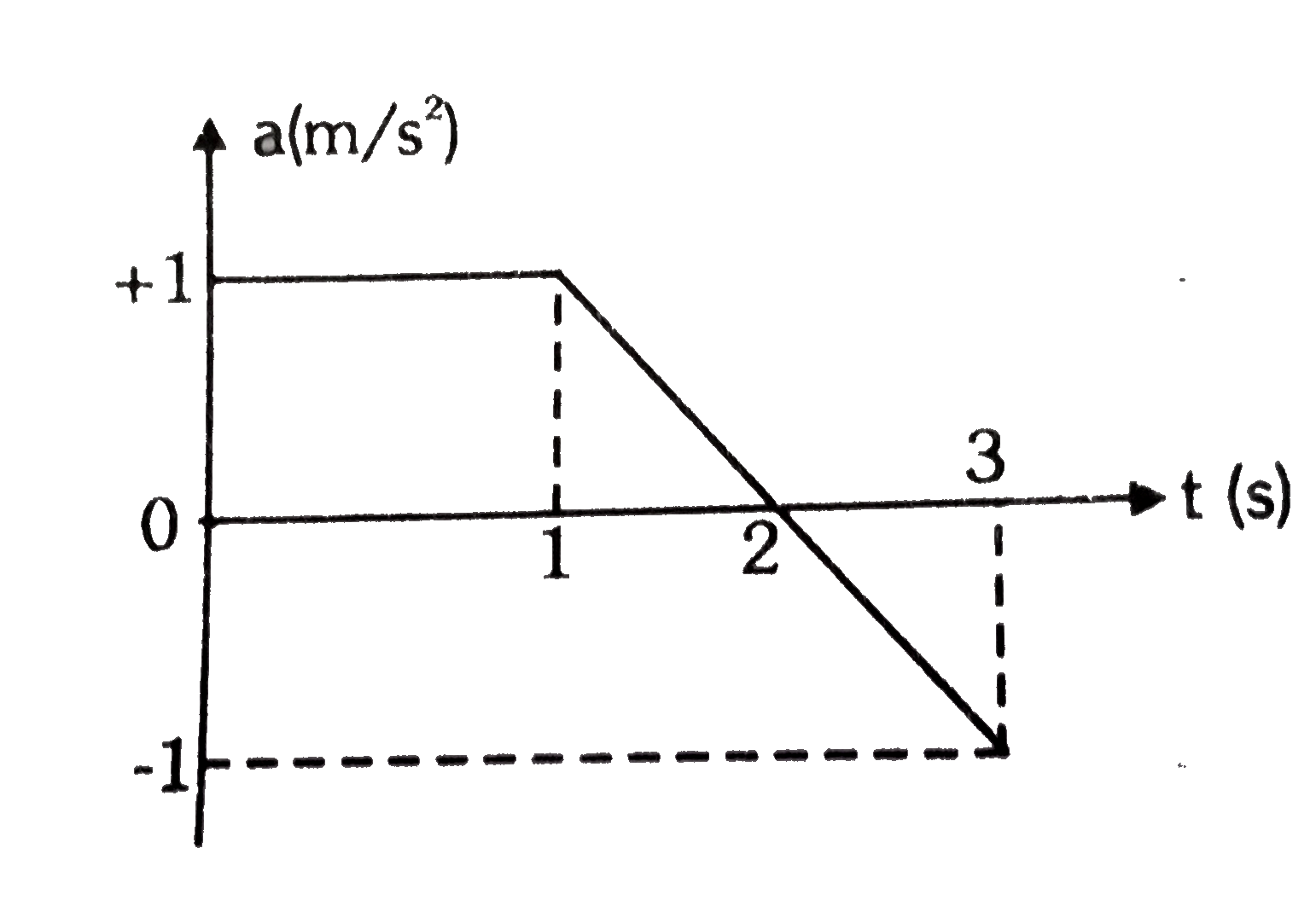
View SolutionA particle at rest starts moving in a horizontal straight line with a uniform acceleration. The ratio of the distances covered during the fourth and third seconds is
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q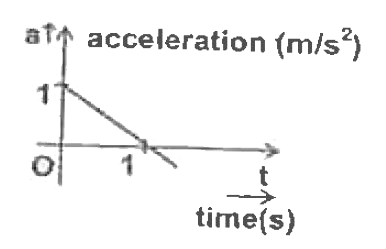
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant

View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View Solution
