The two ends of a spring are displaced along the length of the spring. All displacements have equal magnitudes. In which case or cases the tension or compression in the spring will have as maximum magnitude?
the right end is displaced towards right and the left end towards left
both ends are displaced towards right
both ends are displaced towards left
the right end is displaced towards left and the left end towards right.
The correct Answer is:A, D
To solve the problem of determining in which case the tension or compression in a spring will have the maximum magnitude when the two ends of the spring are displaced along its length, we will analyze each case step by step.
Step 1: Understanding the Spring Force Formula
The force exerted by a spring (either tension or compression) is given by Hooke's Law:
F=k⋅Δx
where:
- F is the force (tension or compression),
- k is the spring constant (a measure of the stiffness of the spring),
- Δx is the change in length of the spring.
Step 2: Analyzing Each Case
We will analyze four different cases based on how the ends of the spring are displaced.
Case 1: Right end displaced to the right and left end displaced to the left
- Displacement of right end = y
- Displacement of left end = y
- Initial length of the spring = L
- Final length = L+y+y=L+2y
- Change in length, Δx=(L+2y)−L=2y
- Force in the spring:
F=k⋅2y
Case 2: Both ends displaced to the right
- Displacement of both ends = y
- Final length = L+y+y=L+2y
- Change in length, Δx=(L+2y)−L=2y
- Force in the spring:
F=k⋅2y
Case 3: Both ends displaced to the left
- Displacement of both ends = y
- Final length = L−y−y=L−2y
- Change in length, Δx=(L−2y)−L=−2y
- Force in the spring:
F=k⋅(−2y)=−2ky
- The magnitude is 2ky.
Case 4: Right end displaced to the left and left end displaced to the right
- Displacement of right end = y (to the left)
- Displacement of left end = y (to the right)
- Final length = L−y+y=L−2y
- Change in length, Δx=(L−2y)−L=−2y
- Force in the spring:
F=k⋅(−2y)=−2ky
- The magnitude is 2ky.
Step 3: Comparing the Magnitudes
From the analysis:
- Case 1: Magnitude of force = 2ky
- Case 2: Magnitude of force = 2ky
- Case 3: Magnitude of force = 2ky
- Case 4: Magnitude of force = 2ky
The maximum magnitude of tension or compression occurs in Case 1 and Case 4, where the spring is either stretched or compressed to the maximum extent.
Conclusion
The cases in which the tension or compression in the spring will have the maximum magnitude are:
- Case 1: Right end displaced to the right and left end displaced to the left.
- Case 4: Right end displaced to the left and left end displaced to the right.
The force exerted by a spring (either tension or compression) is given by Hooke's Law:
F=k⋅Δx
where:
- F is the force (tension or compression),
- k is the spring constant (a measure of the stiffness of the spring),
- Δx is the change in length of the spring.
We will analyze four different cases based on how the ends of the spring are displaced.
- Displacement of right end = y
- Displacement of left end = y
- Initial length of the spring = L
- Final length = L+y+y=L+2y
- Change in length, Δx=(L+2y)−L=2y
- Force in the spring:
F=k⋅2y
- Displacement of both ends = y
- Final length = L+y+y=L+2y
- Change in length, Δx=(L+2y)−L=2y
- Force in the spring:
F=k⋅2y
- Displacement of both ends = y
- Final length = L−y−y=L−2y
- Change in length, Δx=(L−2y)−L=−2y
- Force in the spring:
F=k⋅(−2y)=−2ky
- The magnitude is 2ky.
- Displacement of right end = y (to the left)
- Displacement of left end = y (to the right)
- Final length = L−y+y=L−2y
- Change in length, Δx=(L−2y)−L=−2y
- Force in the spring:
F=k⋅(−2y)=−2ky
- The magnitude is 2ky.
From the analysis:
- Case 1: Magnitude of force = 2ky
- Case 2: Magnitude of force = 2ky
- Case 3: Magnitude of force = 2ky
- Case 4: Magnitude of force = 2ky
The cases in which the tension or compression in the spring will have the maximum magnitude are:
- Case 1: Right end displaced to the right and left end displaced to the left.
- Case 4: Right end displaced to the left and left end displaced to the right.
Topper's Solved these Questions
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Exercises
12 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer
9 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Objective -1
4 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMA ENGLISHCHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - All Questions
75 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
In which of the following cases of motions, the distance moved and the magnitude of displacement are equal ?
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View Solution
Knowledge Check
A rigid rod of length 2L is acted upon by some forces. All forces labelled F have the same magnitude. Which cases have a non-zero net torque acting on the rod about its centre ?
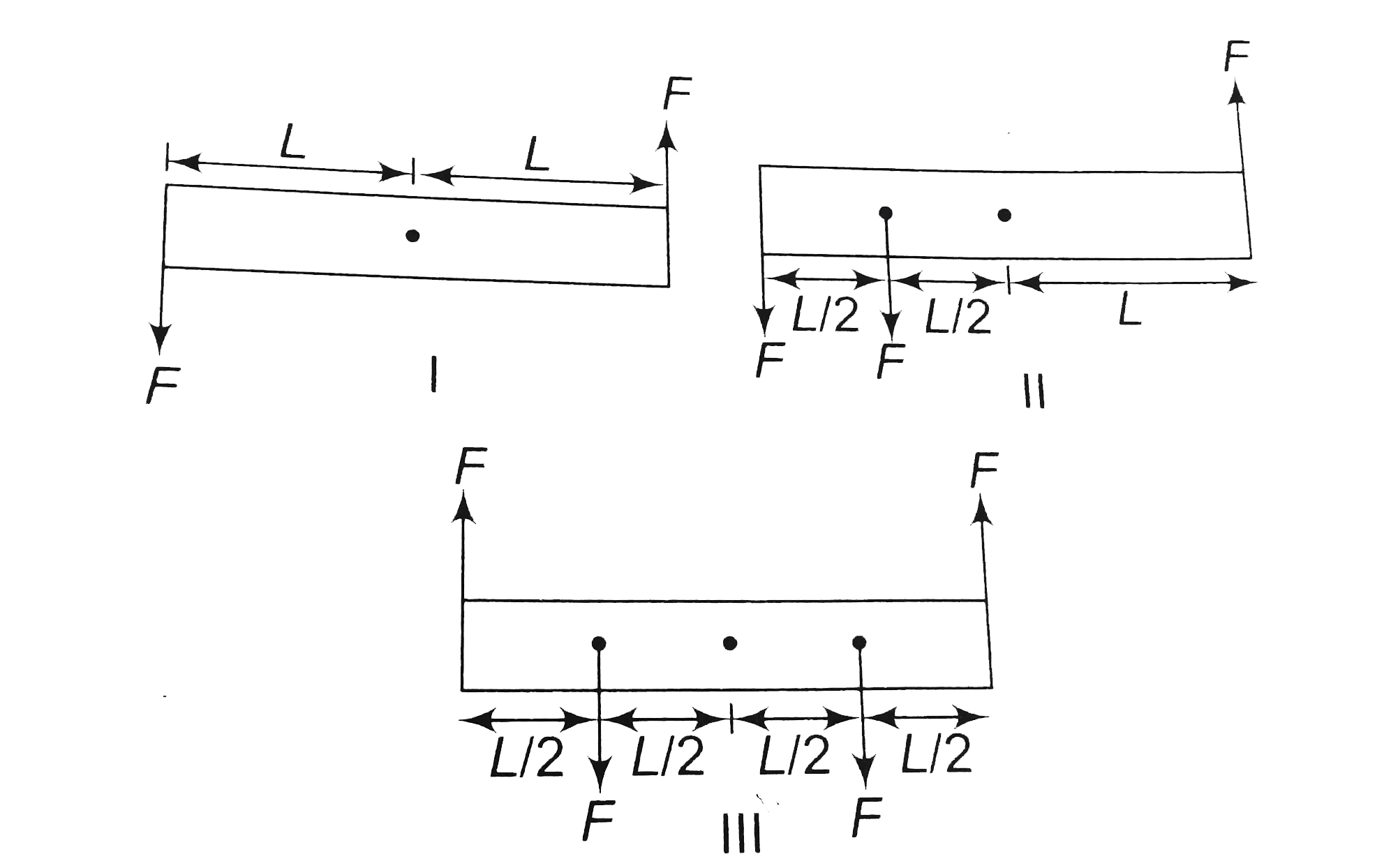 .AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
.AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
Motion of a kink in a longitudinal spring produced by displacing one end of the spring sideways is an example to
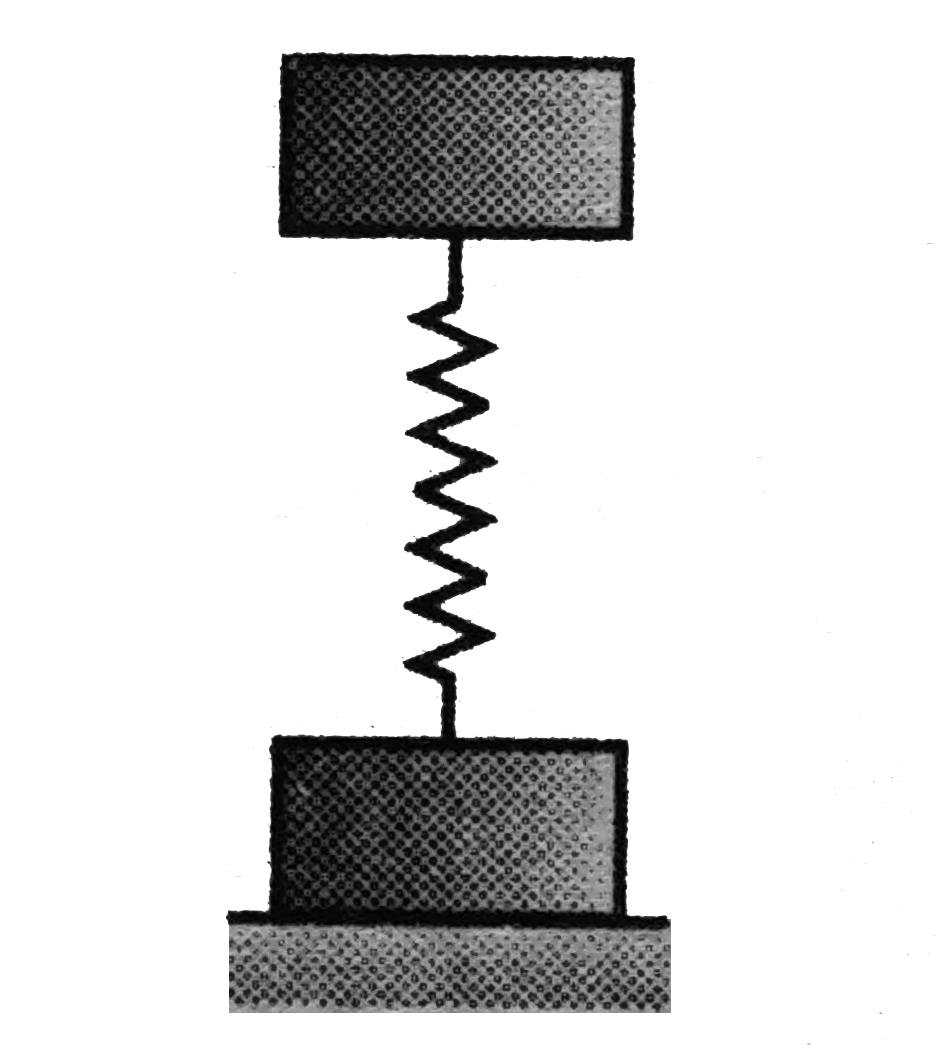
View SolutionTwo discs, each having mass m, are attached rigidly to the ends of a vertical spring. One of the discs rests on a horizontal surface and the other produces a compression x0 on the spring when it is in equilibrium. How much further must the spring be compressed so that when the force causing compression is removed, the extension of the spring will be able to lift the lower disc off the table?
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
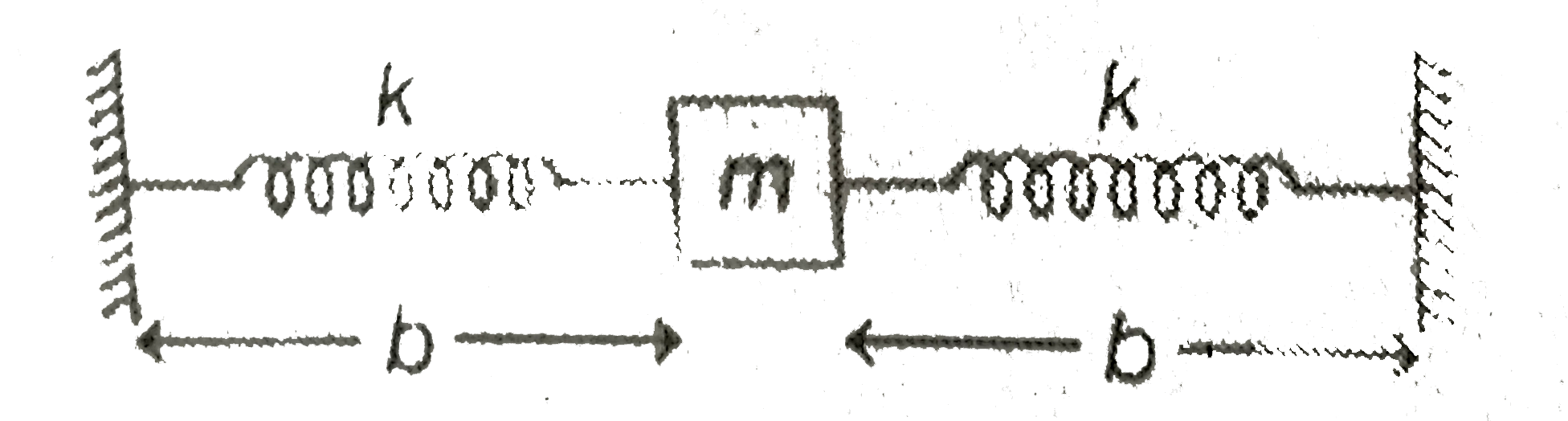
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
View SolutionA srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at x=0. A force of constant magnitude F is applied to the block that begins to compress the spring, until the block comes to a maximum displacement xmax.
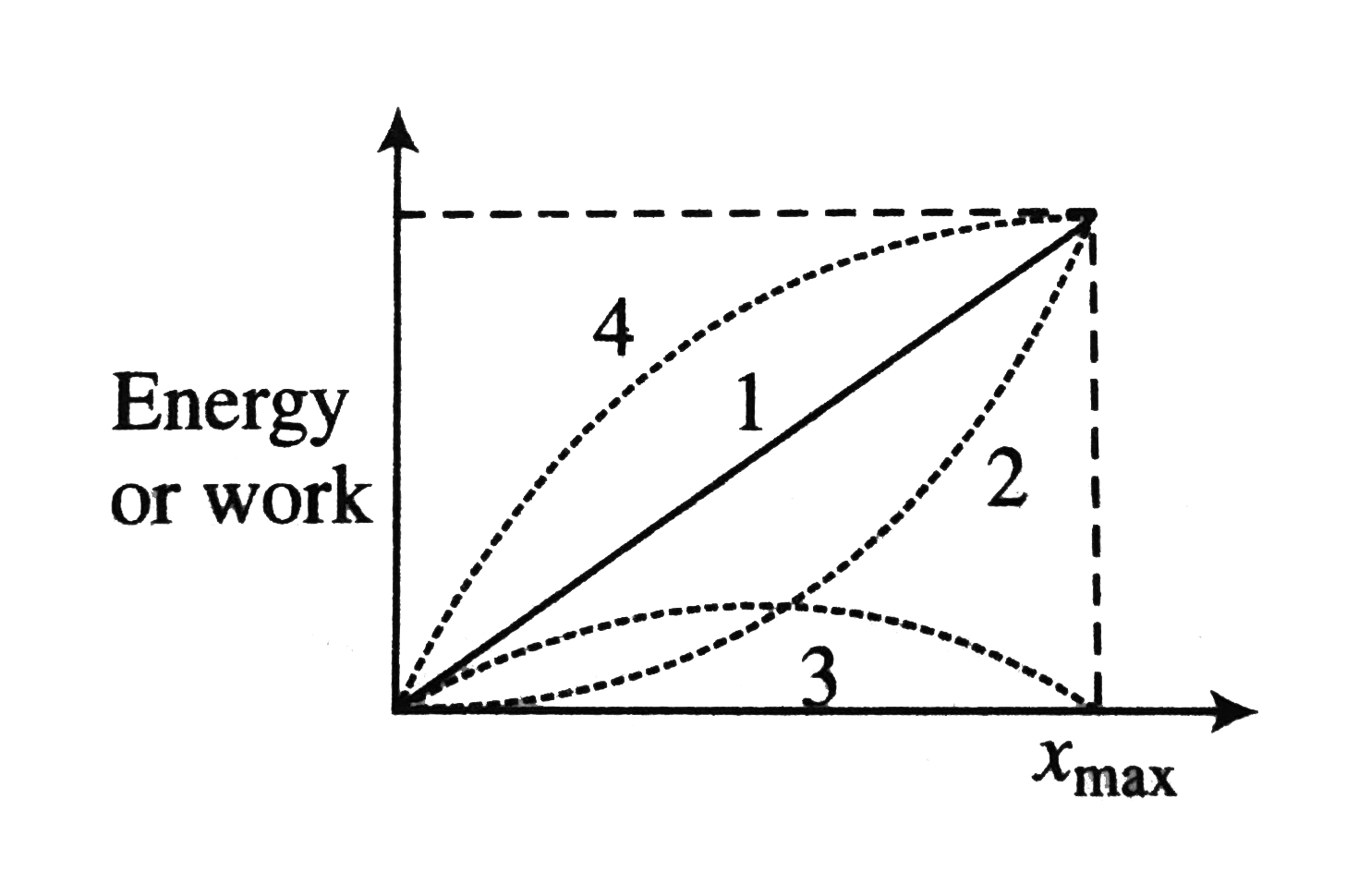
During the displacement, which of the curves shown in the graph best represents the kinetic energy of the block?
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionA srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at x=0. A force of constant magnitude F is applied to the block that begins to compress the spring, until the block comes to a maximum displacement xmax.
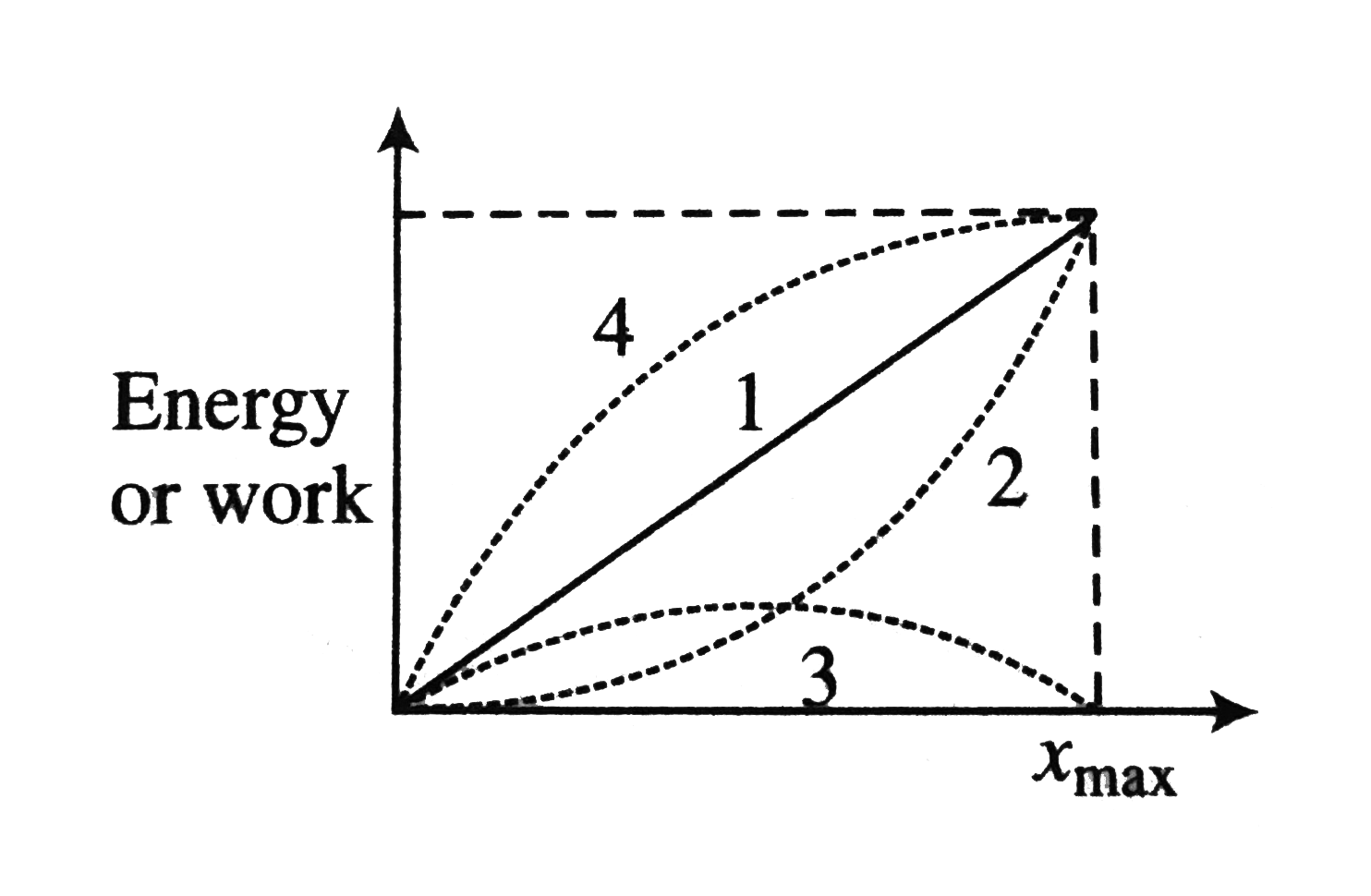
During the displacement, which of the curves shown in the graph best represents the work done on the spring block system by the applied force?
View Solution
