A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
vertical equilibrium
horizontl equilibrium
radia equilibrium
none of these
The correct Answer is:D
To solve the question about the block of mass m sliding down a smooth vertical circular track, we need to analyze the motion of the block and the forces acting on it.
1. Understanding the Motion:
- The block is sliding down a vertical circular track. This means it is moving along a circular path under the influence of gravitational force.
2. Identifying Equilibrium Conditions:
- For an object to be in equilibrium, the net force acting on it must be zero. This applies to vertical, horizontal, and radial (centripetal) directions.
3. Vertical Equilibrium:
- In vertical equilibrium, the acceleration in the vertical direction must be zero. However, as the block slides down, it is influenced by gravitational force mg acting downwards, and there will be a normal force acting perpendicular to the surface of the track. Therefore, the net force in the vertical direction is not zero.
4. Horizontal Equilibrium:
- In horizontal equilibrium, the acceleration in the horizontal direction must also be zero. However, as the block moves along the circular path, it experiences a change in direction, which means there is a centripetal acceleration directed towards the center of the circle. This indicates that the net force in the horizontal direction is not zero.
5. Radial Equilibrium:
- Radial equilibrium refers to the balance of forces in the radial direction (towards the center of the circle). The block experiences a centripetal acceleration given by ar=v2r, where v is the velocity of the block and r is the radius of the circular path. Since the block is moving, v is not zero, and thus the radial acceleration cannot be zero.
6. Conclusion:
- Since the block is not at rest and is continuously accelerating due to gravity and the circular motion, it is clear that the block is not in vertical equilibrium, horizontal equilibrium, or radial equilibrium. Therefore, the correct answer is "none of these."
Final Answer:
The block is in none of these equilibria.
- The block is sliding down a vertical circular track. This means it is moving along a circular path under the influence of gravitational force.
- For an object to be in equilibrium, the net force acting on it must be zero. This applies to vertical, horizontal, and radial (centripetal) directions.
- In vertical equilibrium, the acceleration in the vertical direction must be zero. However, as the block slides down, it is influenced by gravitational force mg acting downwards, and there will be a normal force acting perpendicular to the surface of the track. Therefore, the net force in the vertical direction is not zero.
- In horizontal equilibrium, the acceleration in the horizontal direction must also be zero. However, as the block moves along the circular path, it experiences a change in direction, which means there is a centripetal acceleration directed towards the center of the circle. This indicates that the net force in the horizontal direction is not zero.
- Radial equilibrium refers to the balance of forces in the radial direction (towards the center of the circle). The block experiences a centripetal acceleration given by ar=v2r, where v is the velocity of the block and r is the radius of the circular path. Since the block is moving, v is not zero, and thus the radial acceleration cannot be zero.
- Since the block is not at rest and is continuously accelerating due to gravity and the circular motion, it is clear that the block is not in vertical equilibrium, horizontal equilibrium, or radial equilibrium. Therefore, the correct answer is "none of these."
The block is in none of these equilibria.
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -2
8 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Exercises
64 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Worked out Examples
14 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
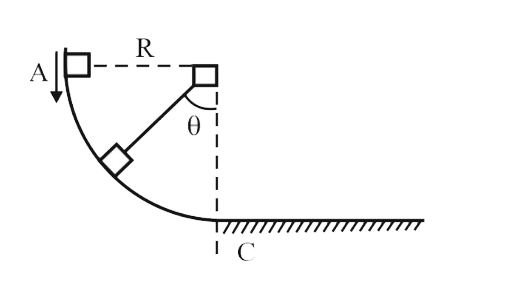
A block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
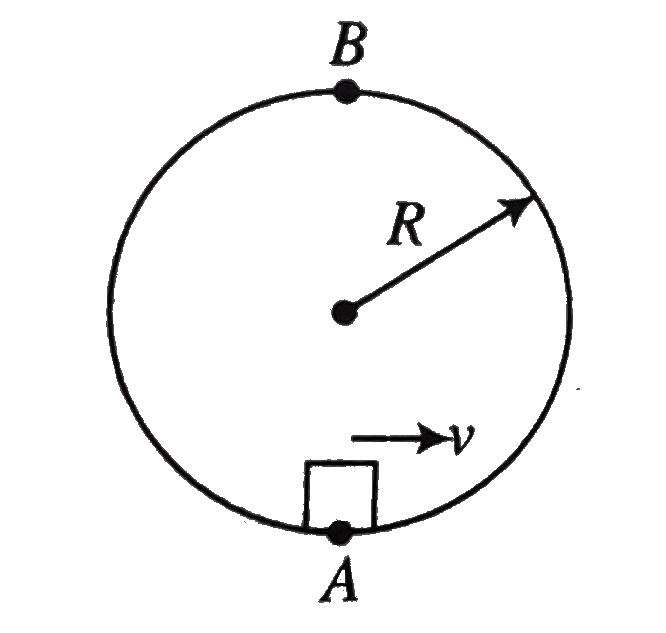
View SolutionA block of mass m is projected on a smooth horizontal circular track with velocity v what is the average normal force exered by the circular walls on the block during motion A to B?
View SolutionA block of mass 1 kg slides down a vertical curved track that is one quadrant of a circle of radius 1m. Its speed ast the the bottom si 2m/s. The work done by frictional force is :

View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2

View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View SolutionA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then

View SolutionA varying horizontal force F= at act on a block of mass m kept on a smooth horizontal surface An identical block is kept on the first block. The coefficient of friction between the blocks is μ . The time after which the relative sliding between the blocks prevails is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
