A block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20J in 1s.
the tension in the string is Mg
The tension is the string is F
The work done by the tension on the block is 20 J in the above 1s.
the work done by the force of gravity is -20J in the above 1s.
The correct Answer is:B
To solve the problem, we need to analyze the situation involving the block, the pulley, and the forces acting on the block. Here's a step-by-step solution:
Step 1: Understand the System
We have a block of mass M hanging over a smooth and light pulley. The other end of the string is being pulled by a constant force F. The block's kinetic energy increases by 20 J in 1 second.
Step 2: Work-Energy Principle
According to the work-energy principle, the work done on an object is equal to the change in its kinetic energy. Therefore, if the kinetic energy of the block increases by 20 J in 1 second, the work done on the block in that time is also 20 J.
Step 3: Calculate the Work Done
The work done W can be expressed as:
W=Fnet⋅d
where Fnet is the net force acting on the block and d is the distance moved by the block in 1 second.
Step 4: Identify Forces Acting on the Block
The forces acting on the block are:
1. The gravitational force Mg acting downwards.
2. The tension T in the string acting upwards.
Since the pulley is smooth and light, we can assume that the tension T is equal to the force F applied at the other end of the string.
Step 5: Set Up the Equation
Using Newton's second law, we can write the equation of motion for the block:
F−Mg=Ma
where a is the acceleration of the block.
Step 6: Relate Work Done to Forces
The net work done on the block can also be expressed as:
W=(T−Mg)⋅d
Since we know W=20J, we can substitute:
20=(F−Mg)⋅d
Step 7: Analyze the Situation
Since the kinetic energy is increasing, the block is accelerating. This means that F must be greater than Mg for the block to move upwards and gain kinetic energy.
Step 8: Conclusion
From our analysis, we can conclude that:
- The work done by the applied force F is responsible for the increase in kinetic energy.
- The tension in the string is equal to the force F applied.
Final Answer
The correct interpretation of the forces and work done leads us to conclude that the work done by the applied force F is 20 J, which results in the increase in kinetic energy of the block.
---
We have a block of mass M hanging over a smooth and light pulley. The other end of the string is being pulled by a constant force F. The block's kinetic energy increases by 20 J in 1 second.
According to the work-energy principle, the work done on an object is equal to the change in its kinetic energy. Therefore, if the kinetic energy of the block increases by 20 J in 1 second, the work done on the block in that time is also 20 J.
The work done W can be expressed as:
W=Fnet⋅d
where Fnet is the net force acting on the block and d is the distance moved by the block in 1 second.
The forces acting on the block are:
1. The gravitational force Mg acting downwards.
2. The tension T in the string acting upwards.
Using Newton's second law, we can write the equation of motion for the block:
F−Mg=Ma
where a is the acceleration of the block.
The net work done on the block can also be expressed as:
W=(T−Mg)⋅d
Since we know W=20J, we can substitute:
20=(F−Mg)⋅d
Since the kinetic energy is increasing, the block is accelerating. This means that F must be greater than Mg for the block to move upwards and gain kinetic energy.
From our analysis, we can conclude that:
- The work done by the applied force F is responsible for the increase in kinetic energy.
- The tension in the string is equal to the force F applied.
The correct interpretation of the forces and work done leads us to conclude that the work done by the applied force F is 20 J, which results in the increase in kinetic energy of the block.
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Exercises
64 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -1
10 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
A block of mass M hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic of the block increases by 40J in 1s. State whether the following statements are true or false.
(a) The tension in the string is Mg .
(b) The work done the tension on the block is 40J.
(c) the tension in the string is F.
(d) The work done by the force of gravity is 40J in the above 1s .
View SolutionA block of mass 10 kg is hanging over a smooth and light pulley through a light string and the other end of the string is pulled down by a constant force F. The kinetic energy of the block increases by 20 J in 1 s
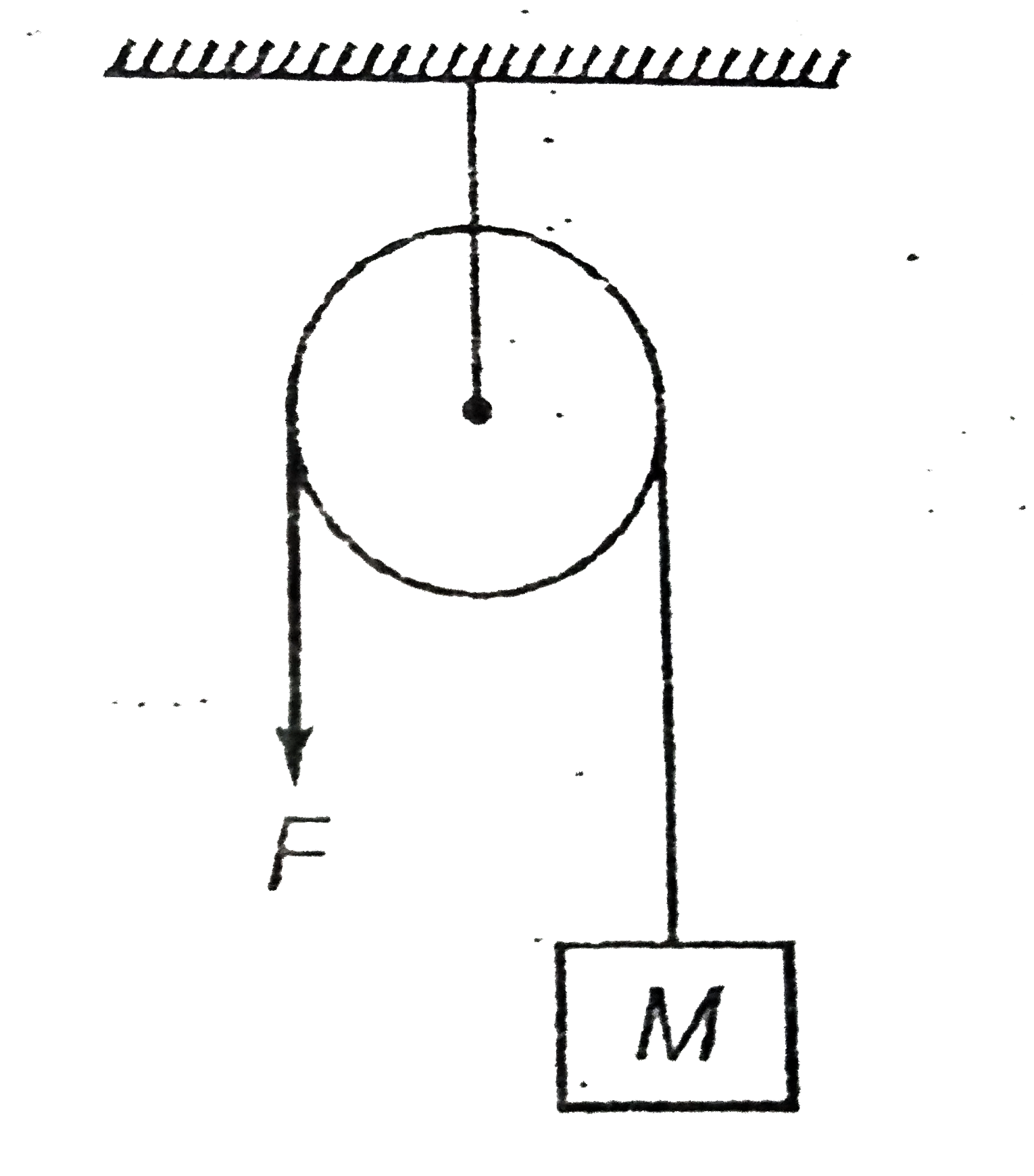
View SolutionA block of mass 2 kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F = 40 N. The kinetic energy of the particle increases 40 J in a given interval of time. Then, (g=10m/s2)
View SolutionA block of mass 2 kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F = 40 N. The kinetic energy of the particle increases 40 J in a given interval of time. Then, (g=10m/s2)
View SolutionA block of mass 2kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F=40N. The kinetic energy of the particle increase 40J in a given interval of time. Then : (g=10m/s2).
 .
.
View SolutionA block of mass 2kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F=40N . At t=0 the system is at rest as shown. Then in the time interval from t=0 to t=2√10 seconds, pick up the correct statement (s):(g=10m/s2)
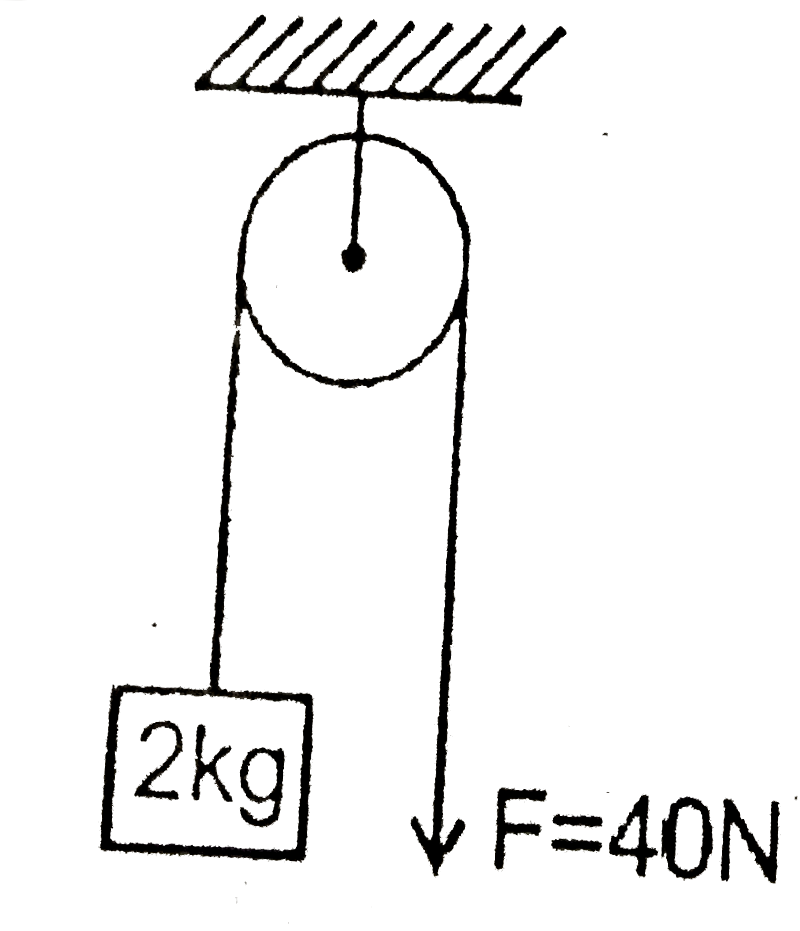
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View SolutionTwo blocks of equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View Solution
