A scooter company gives the following specifications about its product.
Weight of the scooter -95 kg
Maximum speed -60 km/h
Maximum engine power -3.5 hp
Pick up time to get the maximum speed -5s
Check the validity of these specifications.
The correct Answer is:A, B, C, D
To check the validity of the scooter company's specifications, we will go through the following steps:
Step 1: Convert Maximum Speed from km/h to m/s
The maximum speed given is 60 km/h. To convert this to meters per second (m/s), we use the conversion factor:
1 km/h=13.6 m/s
Thus,
60 km/h=60×13.6 m/s=603.6 m/s=60036 m/s=503 m/s≈16.67 m/s
Step 2: Calculate Maximum Acceleration
The scooter reaches its maximum speed in 5 seconds. We can calculate the maximum acceleration using the formula:
Acceleration(a)=Change in VelocityTime=vf−vit
Here, vf=503 m/s, vi=0 m/s, and t=5 s:
a=503−05=5015=103 m/s2≈3.33 m/s2
Step 3: Calculate Force Exerted by the Engine
Using Newton's second law, the force exerted by the engine can be calculated as:
F=m⋅a
Where m=95 kg and a=103 m/s2:
F=95⋅103=9503 N≈316.67 N
Step 4: Convert Engine Power from hp to Watts
The maximum engine power is given as 3.5 hp. To convert this to watts, we use the conversion:
1 hp=746 W
Thus,
Power=3.5×746 W=2611 W
Step 5: Check the Validity of Specifications
To check if the specifications are valid, we will use the relationship between power, force, and velocity:
Power=F⋅v
Rearranging gives us:
v=PowerF
Substituting the values we calculated:
v=26119503=2611⋅3950≈8.25 m/s
Step 6: Compare Maximum Speed with Calculated Speed
The calculated maximum speed from the power and force is approximately 8.25 m/s, while the specified maximum speed is 503≈16.67 m/s. Since 8.25 m/s is significantly less than 16.67 m/s, the specifications provided by the scooter company are not valid.
Conclusion
The specifications of the scooter regarding maximum speed are incorrect based on the calculations performed.
---
The maximum speed given is 60 km/h. To convert this to meters per second (m/s), we use the conversion factor:
1 km/h=13.6 m/s
Thus,
60 km/h=60×13.6 m/s=603.6 m/s=60036 m/s=503 m/s≈16.67 m/s
The scooter reaches its maximum speed in 5 seconds. We can calculate the maximum acceleration using the formula:
Acceleration(a)=Change in VelocityTime=vf−vit
Here, vf=503 m/s, vi=0 m/s, and t=5 s:
a=503−05=5015=103 m/s2≈3.33 m/s2
Using Newton's second law, the force exerted by the engine can be calculated as:
F=m⋅a
Where m=95 kg and a=103 m/s2:
F=95⋅103=9503 N≈316.67 N
The maximum engine power is given as 3.5 hp. To convert this to watts, we use the conversion:
1 hp=746 W
Thus,
Power=3.5×746 W=2611 W
To check if the specifications are valid, we will use the relationship between power, force, and velocity:
Power=F⋅v
Rearranging gives us:
v=PowerF
Substituting the values we calculated:
v=26119503=2611⋅3950≈8.25 m/s
The calculated maximum speed from the power and force is approximately 8.25 m/s, while the specified maximum speed is 503≈16.67 m/s. Since 8.25 m/s is significantly less than 16.67 m/s, the specifications provided by the scooter company are not valid.
The specifications of the scooter regarding maximum speed are incorrect based on the calculations performed.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
A particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
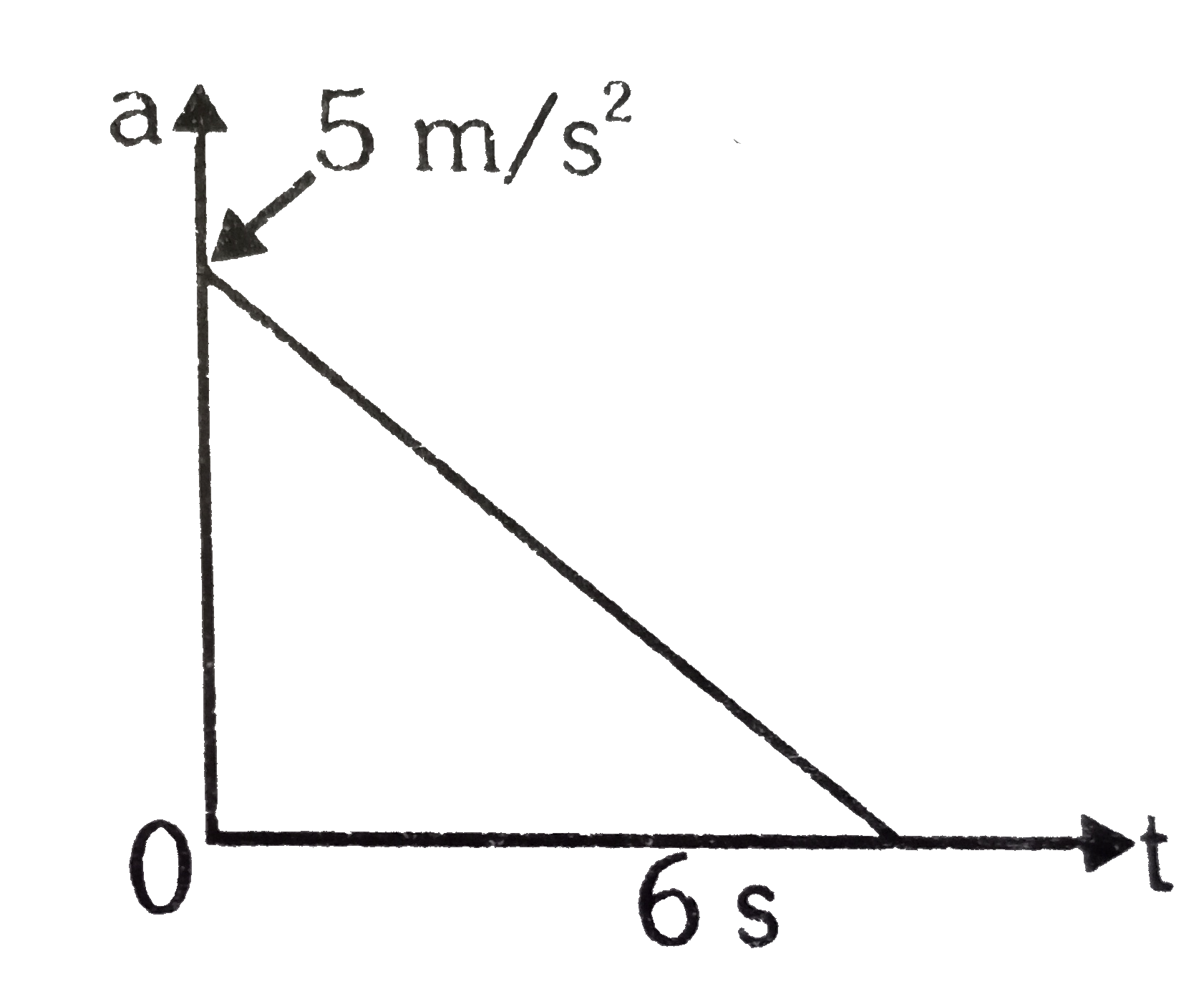 View Solution
View SolutionA child in danger of drowning in a river is being carried downstream by a current that flows uniformly at a speed of 2.5km/h. The child is 0.6 km from shore and 0.8 km upstream of a boat landing when a rescue boat sets out. If the boat proceeds at its maximum speed of 20km/h with respect to the water, what angle does the boat velocity v make with the shore? How long will it take boat to reach the child?
View SolutionA car A is travelling on a straight level road with a uniform speed of 60 km/h. It is followed by another car B which in moving with a speed of 70 km/h. When the distance between then is 2.5km, the car B is given a deceleration of 20kmh2. After how much time will B catch up with A
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?
 View Solution
View SolutionA 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View SolutionThe equation of a particle executing simple harmonic motion is x=(5m)sin[(πs−1)t+π3]. Write down the amplitude time period and maximum speed. Also find the velocity at t=1s.
View SolutionA car A is traveling on a straight level road with a uniform speed of 60 km/h. It is followed by another car B which is moving with a speed of 70 km/h. When the distance between them is 2.5 km, the car B is given a deceleration of 20km/h2. After what distance and time will B catch up with A
View SolutionA string of linear mass density 5.0×10−3 kg//m is stretched under a tension of 65 N between two rigid supports 60 cm apart.
(a) If the string is vibrating in its second overtone so that the amplitude at one of its antinodes is 0.25 cm, what are the maximum transverse speed and acceleration of the string at antinodes?
(b) What are these quantities at a distance 5.0 cm from an node?View SolutionA simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain.
View SolutionA person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s−1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons wieght against time.
(a) Will there be any change in weight of the body, during the oscillation?
(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?View Solution

