A block moving horizontally on a smooth surface with a speed of 20 m/s bursts into two equal parts continuing in the same direction. If one of the parts moves at 30 m/s, with what speed does the second part move and what is the fractional change in the kinetic energy?
To solve the problem step by step, we will follow these steps:
Step 1: Define the initial conditions
Let the initial mass of the block be 2m and its initial velocity be vi=20m/s. After bursting, the block splits into two equal parts, each with mass m. Let the velocities of the two parts be v1 and v2, where we are given v1=30m/s.
Step 2: Apply the principle of conservation of momentum
According to the conservation of momentum, the total momentum before the burst must equal the total momentum after the burst.
The initial momentum pi is:
pi=(2m)⋅(20)=40mkg m/s
The final momentum pf after the burst is:
pf=m⋅v1+m⋅v2=m⋅30+m⋅v2
Setting the initial momentum equal to the final momentum:
40m=30m+mv2
Step 3: Solve for v2
We can simplify the equation by dividing through by m (assuming m≠0):
40=30+v2
v2=40−30=10m/s
Step 4: Calculate the initial kinetic energy
The initial kinetic energy KEi of the system is given by:
KEi=12⋅(2m)⋅(202)=m⋅(202)=400mJ
Step 5: Calculate the final kinetic energy
The final kinetic energy KEf after the burst is:
KEf=12⋅m⋅(v21)+12⋅m⋅(v22)
Substituting the values:
KEf=12⋅m⋅(302)+12⋅m⋅(102)
KEf=12⋅m⋅(900+100)=12⋅m⋅1000=500mJ
Step 6: Calculate the change in kinetic energy
The change in kinetic energy ΔKE is:
ΔKE=KEf−KEi=500m−400m=100mJ
Step 7: Calculate the fractional change in kinetic energy
The fractional change in kinetic energy is given by:
Fractional Change=ΔKEKEi=100m400m=14=0.25
Final Answers
- The speed of the second part v2 is 10m/s.
- The fractional change in kinetic energy is 0.25.
Let the initial mass of the block be 2m and its initial velocity be vi=20m/s. After bursting, the block splits into two equal parts, each with mass m. Let the velocities of the two parts be v1 and v2, where we are given v1=30m/s.
According to the conservation of momentum, the total momentum before the burst must equal the total momentum after the burst.
pi=(2m)⋅(20)=40mkg m/s
pf=m⋅v1+m⋅v2=m⋅30+m⋅v2
40m=30m+mv2
We can simplify the equation by dividing through by m (assuming m≠0):
40=30+v2
v2=40−30=10m/s
The initial kinetic energy KEi of the system is given by:
KEi=12⋅(2m)⋅(202)=m⋅(202)=400mJ
The final kinetic energy KEf after the burst is:
KEf=12⋅m⋅(v21)+12⋅m⋅(v22)
Substituting the values:
KEf=12⋅m⋅(302)+12⋅m⋅(102)
KEf=12⋅m⋅(900+100)=12⋅m⋅1000=500mJ
The change in kinetic energy ΔKE is:
ΔKE=KEf−KEi=500m−400m=100mJ
The fractional change in kinetic energy is given by:
Fractional Change=ΔKEKEi=100m400m=14=0.25
- The speed of the second part v2 is 10m/s.
- The fractional change in kinetic energy is 0.25.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -118videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises64videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -211videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer9videos
CALORIMETRY
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer10videos
CIRCULAR MOTION
Similar Questions
A cart is moving horizontally along a straight line with constant speed 30 m/s. A projectile is to be fired from the moving cart in such a way that it will return to the cart after the cart has moved 120m. At what speed (relative to the cart, in m/s) must the projectile be fired ? (Take g=10m/s2)
View SolutionA projectile moving vertically upwards with a velocity of 200 m/s breaks into two equal parts at the height of 490 m.one part starts moving vertically upwards with a velocity of 400 m/s.How much time after the break up wil the other part hit the ground?
View Solution
Knowledge Check
- Question 1 - Select One
A police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .A95ms−1B105ms−1C115ms−1D125ms−1
.A95ms−1B105ms−1C115ms−1D125ms−1
A police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .View Solution
.View SolutionA police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .View Solution
.View SolutionA projectile is moving at 20ms−1 at its highest point where it breaks into equal parts due to an internal explosion. Just after explosion, one part moves vertically up at 30ms−1 with respect to the ground. Then the other part will move at :
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.
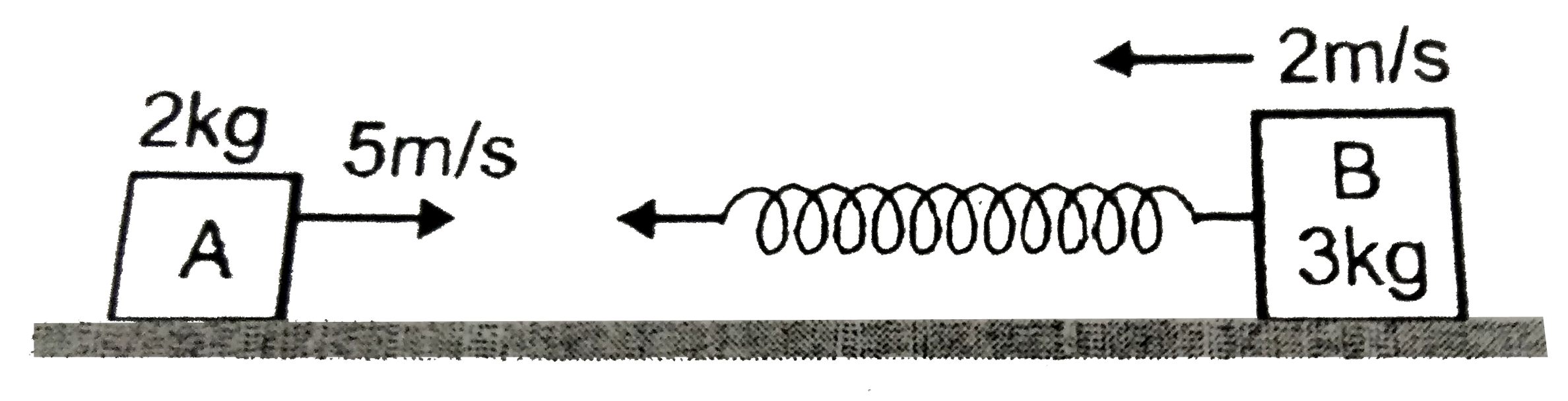
When the blocks are yet to attain their final velocities, in this situation at any instant when block A is moving with a velocity 4ˆim/s , velocity of block B will then be :View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View SolutionWhat is the kinetic energy of a baseball (mass=0.15kg) moving with a speed of 20 m/s?
View Solution

