The moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
The correct Answer is:5
To find the moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centers of two opposite faces, we can follow these steps:
Step 1: Understand the Geometry of the Cube
The hollow cubical box has six square faces. The axis of rotation is passing through the centers of two opposite faces.
Step 2: Moment of Inertia of One Face
The moment of inertia I of a square plate about an axis passing through its center and perpendicular to its plane is given by:
Iface=112ma2
where m is the mass of the square face and a is the side length of the square.
Step 3: Mass of Each Face
Since the total mass M is distributed equally among the six faces, the mass of each face is:
m=M6
Step 4: Calculate Moment of Inertia for One Face
Substituting m into the moment of inertia formula for one face, we get:
Iface=112(M6)a2=Ma272
Step 5: Total Moment of Inertia for Two Faces
Since there are two faces contributing to the moment of inertia about the axis, we multiply by 2:
I1=2×Iface=2×Ma272=Ma236
Step 6: Moment of Inertia of the Side Faces
For the four side faces, we need to use the parallel axis theorem. The moment of inertia of a face about an axis through its center is:
Iside=Icm+Md2
where Icm=112ma2 and d=a2 (the distance from the center of mass to the axis).
Step 7: Calculate Moment of Inertia for One Side Face
Using the mass of each side face m=M6:
Iside=112(M6)a2+(M6)(a2)2
Calculating this gives:
Iside=Ma272+Ma224=Ma272+3Ma272=4Ma272=Ma218
Step 8: Total Moment of Inertia for Four Side Faces
Now, for the four side faces:
I2=4×Iside=4×Ma218=4Ma218=2Ma29
Step 9: Total Moment of Inertia
Finally, the total moment of inertia I about the axis is:
I=I1+I2=Ma236+2Ma29
Finding a common denominator (36):
I=Ma236+8Ma236=9Ma236=Ma24
Final Result
Thus, the moment of inertia of the hollow cubical box about the specified axis is:
Ma24
The hollow cubical box has six square faces. The axis of rotation is passing through the centers of two opposite faces.
The moment of inertia I of a square plate about an axis passing through its center and perpendicular to its plane is given by:
Iface=112ma2
where m is the mass of the square face and a is the side length of the square.
Since the total mass M is distributed equally among the six faces, the mass of each face is:
m=M6
Substituting m into the moment of inertia formula for one face, we get:
Iface=112(M6)a2=Ma272
Since there are two faces contributing to the moment of inertia about the axis, we multiply by 2:
I1=2×Iface=2×Ma272=Ma236
For the four side faces, we need to use the parallel axis theorem. The moment of inertia of a face about an axis through its center is:
Iside=Icm+Md2
where Icm=112ma2 and d=a2 (the distance from the center of mass to the axis).
Using the mass of each side face m=M6:
Iside=112(M6)a2+(M6)(a2)2
Calculating this gives:
Iside=Ma272+Ma224=Ma272+3Ma272=4Ma272=Ma218
Now, for the four side faces:
I2=4×Iside=4×Ma218=4Ma218=2Ma29
Finally, the total moment of inertia I about the axis is:
I=I1+I2=Ma236+2Ma29
Finding a common denominator (36):
I=Ma236+8Ma236=9Ma236=Ma24
Thus, the moment of inertia of the hollow cubical box about the specified axis is:
Ma24
Similar Questions
The moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle θ with the line joining its ends ( as shown ) is
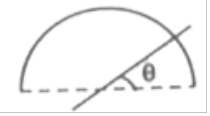
View SolutionIn the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?

View SolutionThe moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionWhy does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmentry ?
View Solution
