A solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
0.8kg-m2
0.4kg-m2
0.2 kg-m2
20.2 kg-m2
The correct Answer is:2
To find the moment of inertia of a solid cylinder about its geometrical axis, we can use the formula:
I=12mr2
where:
- I is the moment of inertia,
- m is the mass of the cylinder,
- r is the radius of the cylinder.
1. Identify the given values:
- Mass m=20kg
- Radius r=0.2m
2. Substitute the values into the moment of inertia formula:
I=12×m×r2
3. Calculate r2:
r2=(0.2m)2=0.04m2
4. Substitute r2 back into the formula:
I=12×20kg×0.04m2
5. Perform the multiplication:
I=12×20×0.04=10×0.04=0.4kg⋅m2
6. Final result:
I=0.4kg⋅m2
Conclusion:
The moment of inertia of the solid cylinder about its geometrical axis is 0.4kg⋅m2.
---
- I is the moment of inertia,
- m is the mass of the cylinder,
- r is the radius of the cylinder.
- Mass m=20kg
- Radius r=0.2m
I=12×m×r2
r2=(0.2m)2=0.04m2
I=12×20kg×0.04m2
I=12×20×0.04=10×0.04=0.4kg⋅m2
I=0.4kg⋅m2
The moment of inertia of the solid cylinder about its geometrical axis is 0.4kg⋅m2.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
A body has mass M and radius 2r. If the body assumes four shapes, solid cylinder, solid sphere, disc and ring of same radius, then the moment of inertia will be maximum about axis through centre of mass for:
View SolutionA silver cylindrical rod has a length of 0.5 m and radius of 0.4 m, find the density of the rod, if its mass is 2640 kg.
View Solution
Knowledge Check
A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
A1:4B3:1C2:3D1:5
A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
View SolutionA bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
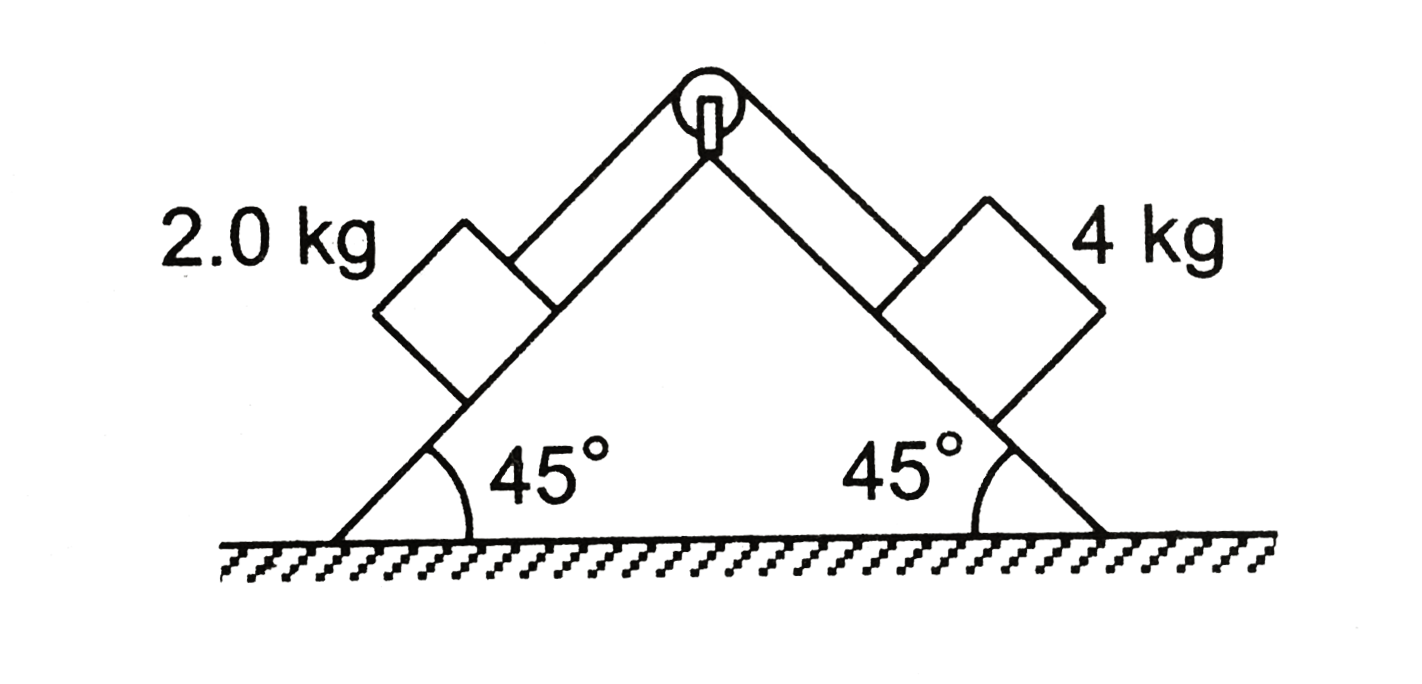
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View Solution