In a laboratory experiment with simple pendulum it was found it took 36 s to complete 20 oscillations when the effective length was kept that 80 cm. Calculate the acceleration due to gravity from these data.
To calculate the acceleration due to gravity using the data from the simple pendulum experiment, we can follow these steps:
1. Determine the Time Period (T):
- The total time for 20 oscillations is given as 36 seconds.
- To find the time period for one oscillation, we divide the total time by the number of oscillations:
T=Total TimeNumber of Oscillations=36 s20=1.8 s
2. Use the Formula for the Time Period of a Simple Pendulum:
- The formula for the time period T of a simple pendulum is given by:
T=2π√Lg
- Rearranging this formula to solve for g:
g=4π2LT2
3. Convert the Length to Meters:
- The effective length L is given as 80 cm. We need to convert this to meters:
L=80 cm=0.8 m
4. Substitute the Values into the Formula:
- Now we can substitute L and T into the rearranged formula:
g=4π2×0.8 m(1.8 s)2
5. Calculate the Value of g:
- First, calculate (1.8)2:
(1.8)2=3.24
- Now, substitute this value into the equation:
g=4×π2×0.83.24
- Using π≈3.14:
g=4×(3.14)2×0.83.24≈4×9.86×0.83.24≈31.3923.24≈9.69 m/s2
6. Final Result:
- Therefore, the calculated acceleration due to gravity g is approximately:
g≈9.69 m/s2
- The total time for 20 oscillations is given as 36 seconds.
- To find the time period for one oscillation, we divide the total time by the number of oscillations:
T=Total TimeNumber of Oscillations=36 s20=1.8 s
- The formula for the time period T of a simple pendulum is given by:
T=2π√Lg
- Rearranging this formula to solve for g:
g=4π2LT2
- The effective length L is given as 80 cm. We need to convert this to meters:
L=80 cm=0.8 m
- Now we can substitute L and T into the rearranged formula:
g=4π2×0.8 m(1.8 s)2
- First, calculate (1.8)2:
(1.8)2=3.24
- Now, substitute this value into the equation:
g=4×π2×0.83.24
- Using π≈3.14:
g=4×(3.14)2×0.83.24≈4×9.86×0.83.24≈31.3923.24≈9.69 m/s2
- Therefore, the calculated acceleration due to gravity g is approximately:
g≈9.69 m/s2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - worked out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
The period P of a simple pendulum is the time for one complete swing. How does P depend on the mass m of the bob, the length l of the string, and the acceleration due to gravity g?
View SolutionCalculate the time period of a simple pendulum of length one meter. The acceleration due to gravity at the place is π2ms−2.
View Solution
Knowledge Check
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
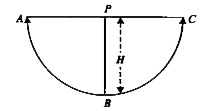 AzeroB2g HCmghD√(2gH)
AzeroB2g HCmghD√(2gH)
A simple pendulum is transferred from the earth to the moon. Assuming its time period is inversely proportional to the square root of acceleration due to gravity, it will
View SolutionThe period of a simple pendulum on the surface of the earth is 2s. Find its period on the surface of this moon, if the acceleration due to gravity on the moon is one-sixth that on the earth ?
View SolutionIn an experiment of simple pendulum , the time period measured was 50sfor25 vibrations when the length of the simple pendulum was taken 100cm. If the least count of stop watch is 0.1s and that of meter scale is 0.1cm. Calculate the maximum possible error in the measurement of value of g. If the actual value of g at the place of experiment is 9.7720ms−2 , Calculate the percentage error.
View SolutionA simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π3 seconds to complete one oscilation. Find the acceleration of the elevator.
View SolutionDerive an expression for the time period (T) of a simple pendulum which may depend upon the mass (m) of the bob, length (l) of the pendulum and acceleration due to gravity (g).
View SolutionA simple pendulum is suspended from the ceiling of a car and its period of oscillation is T when the car is at rest. The car starts moving on a horizontal road with a constant acceleration g (equal to the acceleration due to gravity, in magnitude) in the forward direction. To keep the time period same, the length of th pendulum
View SolutionIn an experiment of simple pendulum the errors in the measurement of length of the pendulum L and time period T are 3% and 2% respectively. Find the maximum percentage error in the value of acceleration due to gravity.
View Solution
